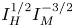Refine search
Actions for selected content:
237510 results in Physics and Astronomy
Turbulent magnetic decay controlled by two conserved quantities
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 03 January 2025, E5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
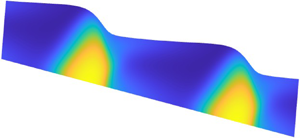
Instability of falling films of discontinuously shear-thickening fluid
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 03 January 2025, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Long-term stable timing fluctuation correction for a picosecond laser with attosecond-level accuracy
-
- Journal:
- High Power Laser Science and Engineering / Volume 12 / 2024
- Published online by Cambridge University Press:
- 03 January 2025, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global drag reduction and local flow statistics in Taylor–Couette turbulence with dilute polymer additives
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 03 January 2025, A33
-
- Article
- Export citation
Structure of mushy layers grown from perfectly and imperfectly conducting boundaries. Part 1. Diffusive solidification
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 03 January 2025, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear coherent structures in 2-D plane Couette flow with constant throughflow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 03 January 2025, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the formation of super-stable granular heaps
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 03 January 2025, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interpretation of the amplitude modulation coefficient and a new transport-based coefficient
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 03 January 2025, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An intermittency based Reynolds-averaged transition model for mixing flows induced by interfacial instabilities
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 03 January 2025, A31
-
- Article
- Export citation

Nonequilibrium Many-Body Theory of Quantum Systems
- A Modern Introduction
-
- Published online:
- 02 January 2025
- Print publication:
- 16 January 2025
Part II - Construction of The Standard Model
-
- Book:
- Uncovering Quantum Field Theory and the Standard Model
- Published online:
- 06 February 2025
- Print publication:
- 02 January 2025, pp 223-398
-
- Chapter
- Export citation
A 606 W burst-mode picosecond Yb-doped all-fiber laser with an intra-burst repetition rate of 469 MHz
-
- Journal:
- High Power Laser Science and Engineering / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 January 2025, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
20 - U(1)A-Problem
- from Part III - Strong Interaction
-
- Book:
- Uncovering Quantum Field Theory and the Standard Model
- Published online:
- 06 February 2025
- Print publication:
- 02 January 2025, pp 442-449
-
- Chapter
- Export citation
Appendix B - Units, Hierarchies, and Fundamental Parameters
-
- Book:
- Uncovering Quantum Field Theory and the Standard Model
- Published online:
- 06 February 2025
- Print publication:
- 02 January 2025, pp 590-597
-
- Chapter
- Export citation
Subject Index
-
- Book:
- Uncovering Quantum Field Theory and the Standard Model
- Published online:
- 06 February 2025
- Print publication:
- 02 January 2025, pp 699-705
-
- Chapter
- Export citation
Reviews
-
- Book:
- Uncovering Quantum Field Theory and the Standard Model
- Published online:
- 06 February 2025
- Print publication:
- 02 January 2025, pp ii-ii
-
- Chapter
- Export citation
Appendix F - Lie Groups and Lie Algebras
-
- Book:
- Uncovering Quantum Field Theory and the Standard Model
- Published online:
- 06 February 2025
- Print publication:
- 02 January 2025, pp 613-640
-
- Chapter
- Export citation
Appendix H - Monte Carlo Method
-
- Book:
- Uncovering Quantum Field Theory and the Standard Model
- Published online:
- 06 February 2025
- Print publication:
- 02 January 2025, pp 648-662
-
- Chapter
- Export citation
Contents
-
- Book:
- Uncovering Quantum Field Theory and the Standard Model
- Published online:
- 06 February 2025
- Print publication:
- 02 January 2025, pp v-xiv
-
- Chapter
- Export citation
Finale
- from Part IV - Selected Topics beyond the Standard Model
-
- Book:
- Uncovering Quantum Field Theory and the Standard Model
- Published online:
- 06 February 2025
- Print publication:
- 02 January 2025, pp 580-582
-
- Chapter
- Export citation