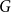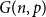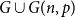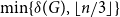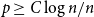Refine search
Actions for selected content:
52379 results in Statistics and Probability
Triangles in randomly perturbed graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 05 July 2022, pp. 91-121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Risk factors for underlying comorbidities and complications in patients with hepatitis B virus-related acute-on-chronic liver failure
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 05 July 2022, e147
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Developing a risk management framework to improve public health outcomes by enumerating Salmonella in ground turkey – RETRACTION
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 04 July 2022, e124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relativistic conceptions of trustworthiness: Implications for the trustworthy status of national identification systems
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 01 July 2022, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Index of Special Symbols
-
- Book:
- Compound Renewal Processes
- Published online:
- 16 June 2022
- Print publication:
- 30 June 2022, pp 363-364
-
- Chapter
- Export citation
16 - Introduction
- from III - Linear Algebra
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp 131-136
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Compound Renewal Processes
- Published online:
- 16 June 2022
- Print publication:
- 30 June 2022, pp i-iv
-
- Chapter
- Export citation
7 - Summary of Part I
- from I - Mathematical Background
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp 61-62
-
- Chapter
- Export citation
13 - Summary of Part II and Further Reading
- from II - Integration
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp 119-122
-
- Chapter
- Export citation
23 - Summary of Part III
- from III - Linear Algebra
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp 193-194
-
- Chapter
- Export citation
42 - So What?
- from VII - The Frontier
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp 351-356
-
- Chapter
- Export citation
40 - Perturbative Solvers
- from VI - Solving Ordinary Differential Equations
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp 331-338
-
- Chapter
- Export citation
2 - Integro-Local Limit Theorems in the Normal Deviation Zone
-
- Book:
- Compound Renewal Processes
- Published online:
- 16 June 2022
- Print publication:
- 30 June 2022, pp 57-89
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp ix-x
-
- Chapter
- Export citation
Dedication
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp v-v
-
- Chapter
- Export citation
V - Global Optimisation
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp 243-244
-
- Chapter
- Export citation
Symbols and Notation
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp xi-xii
-
- Chapter
- Export citation
20 - Computational Constraints
- from III - Linear Algebra
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp 169-174
-
- Chapter
- Export citation
27 - Controlling Optimisation by Probabilistic Estimates
- from IV - Local Optimisation
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp 221-228
-
- Chapter
- Export citation
24 - Key Points
- from IV - Local Optimisation
-
- Book:
- Probabilistic Numerics
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022, pp 197-198
-
- Chapter
- Export citation