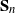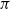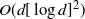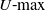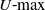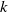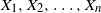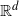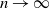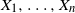Refine search
Actions for selected content:
52379 results in Statistics and Probability
The hit-and-run version of top-to-random
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 12 July 2022, pp. 860-879
- Print publication:
- September 2022
-
- Article
- Export citation
COVID-19 vaccination rollout in the World Health Organization African region: status at end June 2022 and way forward
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 12 July 2022, e143
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Skew brownian motion and complexity of the alps algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 12 July 2022, pp. 777-796
- Print publication:
- September 2022
-
- Article
- Export citation
Application of recommender systems and time series models to monitor quality at HIV/AIDS health facilities
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 11 July 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Author response to: Letter to Editor in Response to the association between contact with children and the clinical course of COVID-19
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 11 July 2022, e139
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A novel approach to estimate the local population denominator to calculate disease incidence for hospital-based health events in England
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 11 July 2022, e150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mutually interacting superprocesses with migration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 904-929
- Print publication:
- September 2022
-
- Article
- Export citation
Generalized limit theorems for U-max statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 825-848
- Print publication:
- September 2022
-
- Article
- Export citation
An extended class of univariate and multivariate generalized Pólya processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 974-997
- Print publication:
- September 2022
-
- Article
- Export citation
A DECOMPOSITION ANALYSIS OF DIFFUSION OVER A LARGE NETWORK
-
- Journal:
- Econometric Theory / Volume 38 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 1221-1252
-
- Article
-
- You have access
- Open access
- Export citation
Asymptotics of the overflow in urn models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 797-824
- Print publication:
- September 2022
-
- Article
- Export citation
Varentropy of doubly truncated random variable
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 852-871
-
- Article
- Export citation
Transmission of SARS-CoV-2 among children and staff in German daycare centres
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 08 July 2022, e141
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Persisting gastrointestinal symptoms and post-infectious irritable bowel syndrome following SARS-CoV-2 infection: results from the Arizona CoVHORT
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 08 July 2022, e136
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On supercritical branching processes with emigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 08 July 2022, pp. 734-754
- Print publication:
- September 2022
-
- Article
- Export citation
Large-time behaviour and the second eigenvalue problem for finite-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 85-125
- Print publication:
- March 2023
-
- Article
- Export citation
The digitization of the Brazilian national identity system: A descriptive and qualitative analysis of its information architecture
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 07 July 2022, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Response to the association between contact with children and the clinical course of COVID-19
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 07 July 2022, e140
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit laws for large
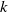 $k$th-nearest neighbor balls
$k$th-nearest neighbor balls
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 July 2022, pp. 880-894
- Print publication:
- September 2022
-
- Article
-
- You have access
- HTML
- Export citation
Clustered colouring of graph classes with bounded treedepth or pathwidth
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 05 July 2022, pp. 122-133
-
- Article
- Export citation