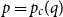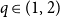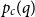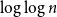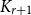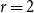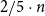Refine search
Actions for selected content:
52379 results in Statistics and Probability
9 - Diagnostics for Logistic Regression
-
- Book:
- Regression for Health and Social Science
- Published online:
- 20 May 2022
- Print publication:
- 12 May 2022, pp 195-211
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Regression for Health and Social Science
- Published online:
- 20 May 2022
- Print publication:
- 12 May 2022, pp i-iv
-
- Chapter
- Export citation
5 - Multiple Regression and Diagnostics
-
- Book:
- Regression for Health and Social Science
- Published online:
- 20 May 2022
- Print publication:
- 12 May 2022, pp 101-129
-
- Chapter
- Export citation
8 - Logistic Regression
-
- Book:
- Regression for Health and Social Science
- Published online:
- 20 May 2022
- Print publication:
- 12 May 2022, pp 178-194
-
- Chapter
- Export citation
6 - Indicators, Interactions, and Transformations
-
- Book:
- Regression for Health and Social Science
- Published online:
- 20 May 2022
- Print publication:
- 12 May 2022, pp 130-159
-
- Chapter
- Export citation
11 - Survival Analysis
-
- Book:
- Regression for Health and Social Science
- Published online:
- 20 May 2022
- Print publication:
- 12 May 2022, pp 233-244
-
- Chapter
- Export citation
3 - Introduction to Linear Regression
-
- Book:
- Regression for Health and Social Science
- Published online:
- 20 May 2022
- Print publication:
- 12 May 2022, pp 64-83
-
- Chapter
- Export citation
Contents
-
- Book:
- Regression for Health and Social Science
- Published online:
- 20 May 2022
- Print publication:
- 12 May 2022, pp v-x
-
- Chapter
- Export citation
Selected Solutions and Hints
-
- Book:
- Regression for Health and Social Science
- Published online:
- 20 May 2022
- Print publication:
- 12 May 2022, pp 266-271
-
- Chapter
- Export citation
7 - Nonparametric Statistics
-
- Book:
- Regression for Health and Social Science
- Published online:
- 20 May 2022
- Print publication:
- 12 May 2022, pp 160-177
-
- Chapter
- Export citation
Preface
-
- Book:
- Regression for Health and Social Science
- Published online:
- 20 May 2022
- Print publication:
- 12 May 2022, pp xi-xiv
-
- Chapter
- Export citation
The critical mean-field Chayes–Machta dynamics
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 11 May 2022, pp. 924-975
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Comorbid conditions as risk factors for West Nile neuroinvasive disease in Ontario, Canada: a population-based cohort study
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 11 May 2022, e103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Introduction to biodiversity valuation tools
-
- Journal:
- British Actuarial Journal / Volume 27 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The importance of biodiversity risks: Link to zoonotic diseases
-
- Journal:
- British Actuarial Journal / Volume 27 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The importance of biodiversity risks
-
- Journal:
- British Actuarial Journal / Volume 27 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Your reserves may be best estimate, but are they valid? (Discussion)
-
- Journal:
- British Actuarial Journal / Volume 27 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Plasmid profile analysis of Escherichia coli and Salmonella enterica isolated from pigs, pork and humans
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The chromatic profile of locally colourable graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 10 May 2022, pp. 976-1009
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The impact of mortality shocks on modelling and insurance valuation as exemplified by COVID-19
-
- Journal:
- Annals of Actuarial Science / Volume 16 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 10 May 2022, pp. 498-526
-
- Article
-
- You have access
- Open access
- HTML
- Export citation