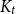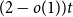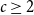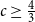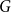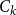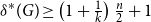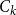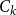Refine search
Actions for selected content:
52379 results in Statistics and Probability
Limit theorems for continuous-state branching processes with immigration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 599-624
- Print publication:
- June 2022
-
- Article
- Export citation
On a random search tree: asymptotic enumeration of vertices by distance from leaves – CORRIGENDUM
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 337-339
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
Normal Approximation for Functions of Hidden Markov Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 536-569
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
Discrete-time risk-aware optimal switching with non-adapted costs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 625-655
- Print publication:
- June 2022
-
- Article
- Export citation
Ruin probabilities with investments: smoothness, inegro-differential and ordinary differential equations, asymptotic behavior
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 June 2022, pp. 556-570
- Print publication:
- June 2022
-
- Article
- Export citation
Risk factors of Shiga toxin-producing Escherichia coli in livestock raised on diversified small-scale farms in California
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 01 June 2022, e125
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On operator fractional Lévy motion: integral representations and time-reversibility
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 493-535
- Print publication:
- June 2022
-
- Article
- Export citation
Nash equilibrium structure of Cox process Hotelling games
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 570-598
- Print publication:
- June 2022
-
- Article
- Export citation
Moment-constrained optimal dividends: precommitment and consistent planning
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 404-432
- Print publication:
- June 2022
-
- Article
- Export citation
Construction of age-structured branching processes by stochastic equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 31 May 2022, pp. 670-684
- Print publication:
- September 2022
-
- Article
-
- You have access
- HTML
- Export citation
Community detection and percolation of information in a geometric setting
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 31 May 2022, pp. 1048-1069
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A large outbreak of COVID-19 in a UK prison, October 2020 to April 2021
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 30 May 2022, e134
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bringing network science to primary school
-
- Journal:
- Network Science / Volume 10 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 207-213
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Consensus embedding for multiple networks: Computation and applications
-
- Journal:
- Network Science / Volume 10 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 190-206
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved lower bound for the list chromatic number of graphs with no Kt minor
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 1070-1075
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transversal Ck-factors in subgraphs of the balanced blow-up of Ck
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 1031-1047
-
- Article
- Export citation
A hierarchical latent space network model for mediation
-
- Journal:
- Network Science / Volume 10 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 113-130
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A pairwise strategic network formation model with group heterogeneity: With an application to international travel
-
- Journal:
- Network Science / Volume 10 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 27 May 2022, pp. 170-189
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lost sales obsolescence inventory systems with positive lead time: a system-point level-crossing approach
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 26 May 2022, pp. 778-800
-
- Article
- Export citation
HIV epidemic amidst COVID-19 pandemic in India: a conundrum for the country's healthcare system
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 26 May 2022, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation