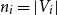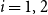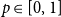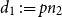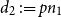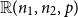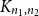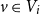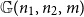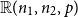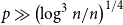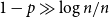Refine search
Actions for selected content:
52379 results in Statistics and Probability
Preface
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp ix-xii
-
- Chapter
- Export citation
Commonly Used Notation
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 238-239
-
- Chapter
- Export citation
5 - Additive Processes
- from Part II - Emergence
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 107-126
-
- Chapter
- Export citation
Index
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 249-250
-
- Chapter
- Export citation
3 - Catastrophes, Conspiracies, and Subexponential Distributions
- from Part I - Properties
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 56-84
-
- Chapter
- Export citation
Incidence and severity of SARS-CoV-2 infection in former Q fever patients as compared to the Dutch population, 2020–2021
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 08 June 2022, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Colouring graphs with forbidden bipartite subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 June 2022, pp. 45-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structural health monitoring of 52-meter wind turbine blade: Detection of damage propagation during fatigue testing
- Part of
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 07 June 2022, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sandwiching biregular random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved bounds for the solutions of renewal equations
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 740-777
-
- Article
- Export citation
Gerber-Shiu analysis in the compound Poisson model with constant inter-observation times
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 324-356
-
- Article
- Export citation
Guiding principles to maintain public trust in the use of mobile operator data for policy purposes – CORRIGENDUM
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 06 June 2022, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HOW LARGE IS THE JUMP DISCONTINUITY IN THE DIFFUSION COEFFICIENT OF A TIME-HOMOGENEOUS DIFFUSION?
-
- Journal:
- Econometric Theory / Volume 39 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 03 June 2022, pp. 848-880
-
- Article
- Export citation
Guidance for Materials 4.0 to interact with a digital twin
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 02 June 2022, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The shape of a seed bank tree
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 June 2022, pp. 631-651
- Print publication:
- September 2022
-
- Article
- Export citation

Probabilistic Numerics
- Computation as Machine Learning
-
- Published online:
- 01 June 2022
- Print publication:
- 30 June 2022
APR volume 54 issue 2 Cover and Back matter
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. b1-b2
- Print publication:
- June 2022
-
- Article
-
- You have access
- Export citation
APR volume 54 issue 2 Cover and Front matter
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. f1-f2
- Print publication:
- June 2022
-
- Article
-
- You have access
- Export citation
A Dynamic Taylor’s law
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 June 2022, pp. 584-607
- Print publication:
- June 2022
-
- Article
- Export citation
On equal-input and monotone Markov matrices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 460-492
- Print publication:
- June 2022
-
- Article
- Export citation