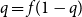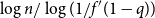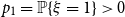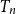Refine search
Actions for selected content:
52379 results in Statistics and Probability
Equivalency of multi-state survival signatures of multi-state systems of different sizes and its use in the comparison of systems
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 10 June 2022, pp. 801-817
-
- Article
- Export citation
ECT volume 38 issue 3 Cover and Front matter
-
- Journal:
- Econometric Theory / Volume 38 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
ECT volume 38 issue 3 Cover and Back matter
-
- Journal:
- Econometric Theory / Volume 38 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Hypergraphs without non-trivial intersecting subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1076-1091
-
- Article
- Export citation
Frontmatter
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp i-iv
-
- Chapter
- Export citation
Part I - Properties
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 27-28
-
- Chapter
- Export citation
Part III - Estimation
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 175-176
-
- Chapter
- Export citation
7 - Extremal Processes
- from Part II - Emergence
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 148-174
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 1-26
-
- Chapter
- Export citation
References
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 240-248
-
- Chapter
- Export citation
2 - Scale Invariance, Power Laws, and Regular Variation
- from Part I - Properties
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 29-55
-
- Chapter
- Export citation
6 - Multiplicative Processes
- from Part II - Emergence
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 127-147
-
- Chapter
- Export citation
Part II - Emergence
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 105-106
-
- Chapter
- Export citation
9 - Estimating Power-Law Tails: Let the Tail Do the Talking
- from Part III - Estimation
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 197-237
-
- Chapter
- Export citation
On the peel number and the leaf-height of Galton–Watson trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 68-90
-
- Article
- Export citation
AAS Thematic issue: “Mortality: from Lee–Carter to AI”
-
- Journal:
- Annals of Actuarial Science / Volume 17 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 212-214
-
- Article
-
- You have access
- HTML
- Export citation
Acknowledgments
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp xiii-xiv
-
- Chapter
- Export citation
4 - Residual Lives, Hazard Rates, and Long Tails
- from Part I - Properties
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 85-104
-
- Chapter
- Export citation
8 - Estimating Power-Law Distributions: Listen to the Body
- from Part III - Estimation
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp 177-196
-
- Chapter
- Export citation
Contents
-
- Book:
- The Fundamentals of Heavy Tails
- Published online:
- 17 May 2022
- Print publication:
- 09 June 2022, pp v-viii
-
- Chapter
- Export citation