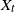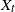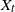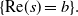Refine search
Actions for selected content:
52385 results in Statistics and Probability
COVID-19 data reporting systems in Africa reveal insights for future pandemics
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 16 June 2022, e119
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generating weighted and thresholded gene coexpression networks using signed distance correlation
-
- Journal:
- Network Science / Volume 10 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 16 June 2022, pp. 131-145
-
- Article
- Export citation
MORTALITY CREDITS WITHIN LARGE SURVIVOR FUNDS
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 52 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 813-834
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unbiased filtering of a class of partially observed diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 661-687
- Print publication:
- September 2022
-
- Article
- Export citation
Raw milk special collection
- Part of
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 15 June 2022, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral analysis of bilateral birth–death processes: some new explicit examples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 1193-1221
- Print publication:
- December 2022
-
- Article
- Export citation
Non-asymptotic control of the cumulative distribution function of Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 913-944
- Print publication:
- September 2022
-
- Article
- Export citation
Temporal changes in the proportion of Salmonella outbreaks associated with 12 food commodity groups in the United States
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 15 June 2022, e126
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gradient estimation for smooth stopping criteria
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 15 June 2022, pp. 29-55
- Print publication:
- March 2023
-
- Article
- Export citation
Central limit theorem for bifurcating markov chains under L2-ergodic conditions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 999-1031
- Print publication:
- December 2022
-
- Article
- Export citation
Measuring reciprocity in a directed preferential attachment network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 718-742
- Print publication:
- September 2022
-
- Article
- Export citation
Extended reduced-form framework for non-life insurance
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 945-973
- Print publication:
- September 2022
-
- Article
- Export citation
Some results on the telegraph process driven by gamma components
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 808-848
- Print publication:
- September 2022
-
- Article
- Export citation
Moments of Markovian growth–collapse processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1070-1093
- Print publication:
- December 2022
-
- Article
- Export citation
Exponential and gamma form for tail expansions of first-passage distributions in semi-markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1291-1319
- Print publication:
- December 2022
-
- Article
- Export citation
Optimal consumption with Hindy–Huang–Kreps preferences under nonlinear expectations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1222-1251
- Print publication:
- December 2022
-
- Article
- Export citation
Probability of total domination for transient reflecting processes in a quadrant
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1094-1138
- Print publication:
- December 2022
-
- Article
- Export citation
ESTIMATION OF A HIGH-DIMENSIONAL COUNTING PROCESS WITHOUT PENALTY FOR HIGH-FREQUENCY EVENTS
-
- Journal:
- Econometric Theory / Volume 39 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 14 June 2022, pp. 989-1008
-
- Article
-
- You have access
- Open access
- Export citation
Conditions for indexability of restless bandits and an
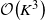 $\mathcal{O}\!\left(K^3\right)$ algorithm to compute Whittle index
$\mathcal{O}\!\left(K^3\right)$ algorithm to compute Whittle index
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1164-1192
- Print publication:
- December 2022
-
- Article
- Export citation
Universal Digital Twin: Integration of national-scale energy systems and climate data
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 13 June 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation