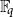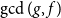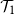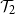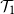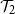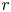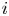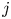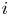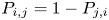Refine search
Actions for selected content:
52379 results in Statistics and Probability
4 - Analyzing Continuous Data
- from II - The Right Statistical Test for Different Types of Data
-
- Book:
- Statistics for Laboratory Scientists and Clinicians
- Published online:
- 17 June 2021
- Print publication:
- 08 July 2021, pp 61-78
-
- Chapter
- Export citation
Contents
-
- Book:
- Statistics for Laboratory Scientists and Clinicians
- Published online:
- 17 June 2021
- Print publication:
- 08 July 2021, pp v-x
-
- Chapter
- Export citation
6 - Analyses for Non-continuous Data
- from II - The Right Statistical Test for Different Types of Data
-
- Book:
- Statistics for Laboratory Scientists and Clinicians
- Published online:
- 17 June 2021
- Print publication:
- 08 July 2021, pp 85-96
-
- Chapter
- Export citation
Preface
-
- Book:
- Statistics for Laboratory Scientists and Clinicians
- Published online:
- 17 June 2021
- Print publication:
- 08 July 2021, pp xi-xiii
-
- Chapter
-
- You have access
- HTML
- Export citation
II - The Right Statistical Test for Different Types of Data
-
- Book:
- Statistics for Laboratory Scientists and Clinicians
- Published online:
- 17 June 2021
- Print publication:
- 08 July 2021, pp 59-110
-
- Chapter
- Export citation
2 - Types of Data and their Distributions
- from I - Basic Statistical Concepts
-
- Book:
- Statistics for Laboratory Scientists and Clinicians
- Published online:
- 17 June 2021
- Print publication:
- 08 July 2021, pp 22-29
-
- Chapter
- Export citation
1 - Understanding Some Basic Statistical Concepts
- from I - Basic Statistical Concepts
-
- Book:
- Statistics for Laboratory Scientists and Clinicians
- Published online:
- 17 June 2021
- Print publication:
- 08 July 2021, pp 3-21
-
- Chapter
- Export citation
Glossary
-
- Book:
- Statistics for Laboratory Scientists and Clinicians
- Published online:
- 17 June 2021
- Print publication:
- 08 July 2021, pp 153-158
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Statistics for Laboratory Scientists and Clinicians
- Published online:
- 17 June 2021
- Print publication:
- 08 July 2021, pp xiv-xiv
-
- Chapter
- Export citation
10 - Interpreting Graphs and Charts
- from III - Applied Statistics
-
- Book:
- Statistics for Laboratory Scientists and Clinicians
- Published online:
- 17 June 2021
- Print publication:
- 08 July 2021, pp 143-152
-
- Chapter
- Export citation
9 - Applied Statistics for the Clinician
- from III - Applied Statistics
-
- Book:
- Statistics for Laboratory Scientists and Clinicians
- Published online:
- 17 June 2021
- Print publication:
- 08 July 2021, pp 135-142
-
- Chapter
- Export citation
Xanthene-stained nanoparticles for phosphorescence anisotropy measurements
-
- Journal:
- Experimental Results / Volume 2 / 2021
- Published online by Cambridge University Press:
- 07 July 2021, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Average-case complexity of the Euclidean algorithm with a fixed polynomial over a finite field
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 166-183
-
- Article
- Export citation
On directed analogues of expander and hyperfinite graph sequences
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 184-197
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuous phase transitions on Galton–Watson trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 198-228
-
- Article
- Export citation
SARS-CoV-2 seroprevalence among employees of a university hospital in Belgium during the 2020 COVID-19 outbreak (COVEMUZ-study)
-
- Journal:
- Epidemiology & Infection / Volume 149 / 2021
- Published online by Cambridge University Press:
- 05 July 2021, e165
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The accuracy versus interpretability trade-off in fraud detection model
-
- Journal:
- Data & Policy / Volume 3 / 2021
- Published online by Cambridge University Press:
- 05 July 2021, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIVERSIFICATION IN CATASTROPHE INSURANCE MARKETS
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 51 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 02 July 2021, pp. 753-778
- Print publication:
- September 2021
-
- Article
- Export citation
TAIL DEPENDENCE OF OLS
-
- Journal:
- Econometric Theory / Volume 38 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 02 July 2021, pp. 273-300
-
- Article
-
- You have access
- Open access
- Export citation
Team's seasonal win probabilities
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 02 July 2021, pp. 988-998
-
- Article
- Export citation