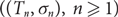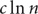Refine search
Actions for selected content:
52383 results in Statistics and Probability
A non-increasing tree growth process for recursive trees and applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 19 October 2020, pp. 79-104
-
- Article
- Export citation

Asymptotic Analysis of Random Walks
- Light-Tailed Distributions
-
- Published online:
- 16 October 2020
- Print publication:
- 29 October 2020
Isolation concepts applied to temporal clique enumeration
-
- Journal:
- Network Science / Volume 9 / Issue S1 / October 2021
- Published online by Cambridge University Press:
- 16 October 2020, pp. S83-S105
-
- Article
- Export citation
Enhancing industrial X-ray tomography by data-centric statistical methods
-
- Journal:
- Data-Centric Engineering / Volume 1 / 2020
- Published online by Cambridge University Press:
- 16 October 2020, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dedication
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp v-vi
-
- Chapter
- Export citation
10 - Proportionally Fair Resource Allocation
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp 219-251
-
- Chapter
- Export citation
12 - Multihop Packet Networks
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp 268-310
-
- Chapter
- Export citation
Contents
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp vii-x
-
- Chapter
- Export citation
Predictors of mortality among multidrug-resistant tuberculosis patients in central Ethiopia: a retrospective follow-up study
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 15 October 2020, e258
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - Introduction
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp 1-28
-
- Chapter
- Export citation
Appendix E - Markovian Arrival Processes
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp 362-368
-
- Chapter
- Export citation
2 - Stochastic Processing Networks
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp 29-53
-
- Chapter
- Export citation
Appendix B - Selected Topics in Probability
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp 319-330
-
- Chapter
- Export citation
Website
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp xi-xii
-
- Chapter
- Export citation
Appendix C - Discrete-Time Markov Chains
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp 331-343
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp i-iv
-
- Chapter
- Export citation
4 - Extensions and Complements
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp 79-106
-
- Chapter
- Export citation
References
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp 371-378
-
- Chapter
- Export citation
Effect of Rinsing Canned Foods on Bisphenol-A Exposure: The Hummus Experiment
-
- Journal:
- Experimental Results / Volume 1 / 2020
- Published online by Cambridge University Press:
- 15 October 2020, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Appendix A - Selected Topics in Real Analysis
-
- Book:
- Processing Networks
- Published online:
- 17 September 2020
- Print publication:
- 15 October 2020, pp 311-318
-
- Chapter
- Export citation