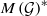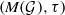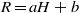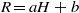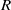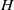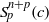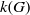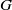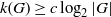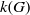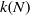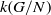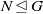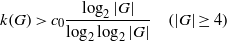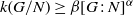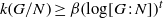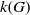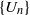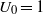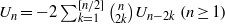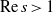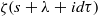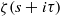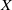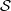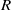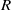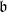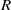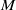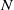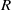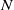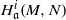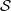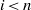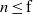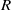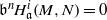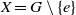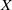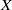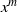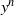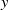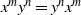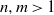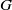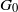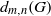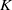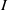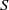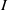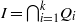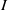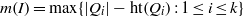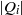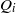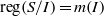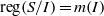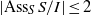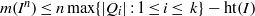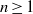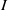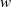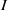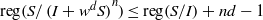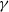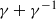Contents
Research Article
THE STRONG DUAL OF MEASURE ALGEBRAS WITH CERTAIN LOCALLY CONVEX TOPOLOGIES
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2013, pp. 353-365
-
- Article
-
- You have access
- Export citation
EXISTENCE RESULTS FOR A CLASS OF ABSTRACT IMPULSIVE DIFFERENTIAL EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2013, pp. 366-385
-
- Article
-
- You have access
- Export citation
COMPLETE SPACELIKE SUBMANIFOLDS IN DE SITTER SPACES WITH
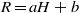 $R= aH+ b$
$R= aH+ b$
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2013, pp. 386-399
-
- Article
-
- You have access
- Export citation
ON THE POSITIVITY OF RIEMANN–STIELTJES INTEGRALS
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2012, pp. 400-405
-
- Article
-
- You have access
- Export citation
NEW REDUCTIONS AND LOGARITHMIC LOWER BOUNDS FOR THE NUMBER OF CONJUGACY CLASSES IN FINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2012, pp. 406-424
-
- Article
-
- You have access
- Export citation
SOME PROPERTIES OF A SEQUENCE ANALOGOUS TO EULER NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 12 June 2012, pp. 425-440
-
- Article
-
- You have access
- Export citation
ON THE ORDER OF ARC-STABILISERS IN ARC-TRANSITIVE GRAPHS, II
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2012, pp. 441-447
-
- Article
-
- You have access
- Export citation
NOTE ON ODD MULTIPERFECT NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2012, pp. 448-451
-
- Article
-
- You have access
- Export citation
SELF-APPROXIMATION FOR THE RIEMANN ZETA FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 31 October 2012, pp. 452-461
-
- Article
-
- You have access
- Export citation
CENTRALISERS IN THE INFINITE SYMMETRIC INVERSE SEMIGROUP
- Part of:
-
- Published online by Cambridge University Press:
- 28 September 2012, pp. 462-479
-
- Article
-
- You have access
- Export citation
LOCAL-GLOBAL PRINCIPLE FOR THE FINITENESS AND ARTINIANNESS OF GENERALISED LOCAL COHOMOLOGY MODULES
- Part of:
-
- Published online by Cambridge University Press:
- 20 August 2012, pp. 480-492
-
- Article
-
- You have access
- Export citation
NOTES ON
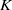 $K$-TOPOLOGICAL GROUPS AND HOMEOMORPHISMS OF TOPOLOGICAL GROUPS
$K$-TOPOLOGICAL GROUPS AND HOMEOMORPHISMS OF TOPOLOGICAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2012, pp. 493-502
-
- Article
-
- You have access
- Export citation
THE PROBABILITY THAT
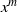 $\lowercase {X}^{\lowercase {M}}$ AND
$\lowercase {X}^{\lowercase {M}}$ AND 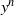 $\lowercase {Y}^{\lowercase {N}}$ COMMUTE IN A COMPACT GROUP
$\lowercase {Y}^{\lowercase {N}}$ COMMUTE IN A COMPACT GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2012, pp. 503-513
-
- Article
-
- You have access
- Export citation
ON A CLASS OF MONOMIAL IDEALS
- Part of:
-
- Published online by Cambridge University Press:
- 28 January 2013, pp. 514-526
-
- Article
-
- You have access
- Export citation
Correction
‘SUM-PRODUCT ESTIMATES AND MULTIPLICATIVE ORDERS OF
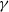 $\gamma $ AND
$\gamma $ AND 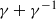 $\gamma + {\gamma }^{- 1} $ IN FINITE FIELDS’
$\gamma + {\gamma }^{- 1} $ IN FINITE FIELDS’
-
- Published online by Cambridge University Press:
- 21 February 2013, pp. 527-528
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
BAZ VOLUME 87 ISSUE 3 COVER AND FRONT MATTER
-
- Published online by Cambridge University Press:
- 21 May 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
BAZ VOLUME 87 ISSUE 3 COVER AND BACK MATTER
-
- Published online by Cambridge University Press:
- 21 May 2013, pp. b1-b10
-
- Article
-
- You have access
- Export citation