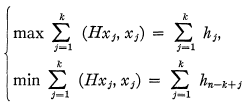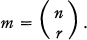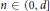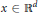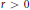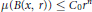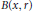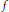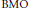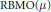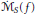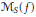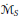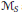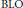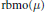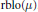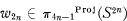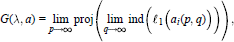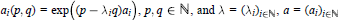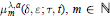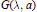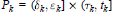Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 3
Green's Functions for Powers of the Invariant Laplacian
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 40-73
-
- Article
-
- You have access
- Export citation
- Cited by 3
Sufficiency Conditions for the Existence of Transversals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 948-961
-
- Article
-
- You have access
- Export citation
- Cited by 3
Isometric Group Actions on Hilbert Spaces: Structure of Orbits
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1001-1009
-
- Article
-
- You have access
- Export citation
- Cited by 3
General Preservers of Quasi-Commutativity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 758-786
-
- Article
-
- You have access
- Export citation
- Cited by 3
Linear Combinations of Composition Operators on the Bloch Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 862-877
-
- Article
-
- You have access
- Export citation
- Cited by 3
Bol Loops of Nilpotence Class Two
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 296-310
-
- Article
-
- You have access
- Export citation
- Cited by 3
Tensor Products of Fundamental Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 633-648
-
- Article
-
- You have access
- Export citation
- Cited by 3
The 2-Rank of the Class Group of Imaginary Bicyclic Biquadratic Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 283-300
-
- Article
-
- You have access
- Export citation
- Cited by 3
Representation Formulas for Integrable and Entire Functions of Exponential Type II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 34-47
-
- Article
-
- You have access
- Export citation
- Cited by 3
On the Unitary Equivalence of Certain Classes of Non-Normal Operators. I
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 849-856
-
- Article
-
- You have access
- Export citation
- Cited by 3
A New Viewpoint in Differential Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 460-470
-
- Article
-
- You have access
- Export citation
- Cited by 3
On a Transformation Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 935-941
-
- Article
-
- You have access
- Export citation
- Cited by 3
Extremal Properties of Hermitian Matrices. II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 379-382
-
- Article
-
- You have access
- Export citation
- Cited by 3
BMO-Estimates for Maximal Operators via Approximations of the Identity with Non-Doubling Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1419-1434
-
- Article
-
- You have access
- Export citation
- Cited by 3
Absolute Approximate Retracts and AR-Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 297-301
-
- Article
-
- You have access
- Export citation
- Cited by 3
Even Whitehead Squares are Not Projective
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 957-962
-
- Article
-
- You have access
- Export citation
- Cited by 3
On Computable Field Embeddings and Difference Closed Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1338-1363
-
- Article
-
- You have access
- Export citation
- Cited by 3
Compound Invariants and Mixed F-, DF-Power Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1138-1162
-
- Article
-
- You have access
- Export citation
- Cited by 3
On The Number of Classes of a Finite Group Invariant for Certain Substitutions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1090-1097
-
- Article
-
- You have access
- Export citation
- Cited by 3
Pure Subfields of Purely Inseparable Field Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1162-1166
-
- Article
-
- You have access
- Export citation
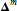
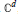
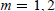
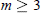
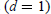
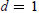
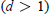
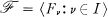 is a 1-1 map
is a 1-1 map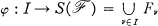
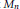

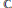
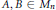
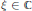
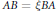
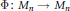
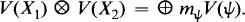
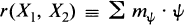
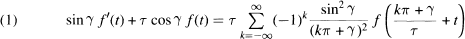
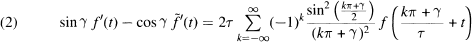
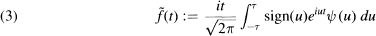
 , determine whether or not they are unitarily equivalent, i.e., whether or not there is a unitary operator
, determine whether or not they are unitarily equivalent, i.e., whether or not there is a unitary operator 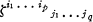

 . We assume furthermore that
. We assume furthermore that