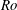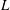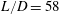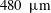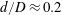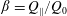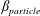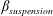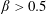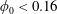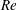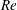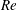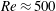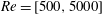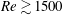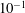Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 14
Low- and mid-frequency wall-pressure sources in a turbulent boundary layer
-
- Published online by Cambridge University Press:
- 07 May 2021, A18
-
- Article
- Export citation
- Cited by 14
The motion of a freely floating cylinder in the presence of a wall and the approximation of resonances
-
- Published online by Cambridge University Press:
- 19 April 2016, pp. 581-610
-
- Article
- Export citation
- Cited by 14
A high-order asymptotic analysis of the Benjamin–Feir instability spectrum in arbitrary depth
-
- Published online by Cambridge University Press:
- 08 February 2023, A29
-
- Article
- Export citation
- Cited by 14
Evolution of similarity lengths in anisotropic magnetohydrodynamic turbulence
-
- Published online by Cambridge University Press:
- 31 July 2019, pp. 5-18
-
- Article
- Export citation
- Cited by 14
Attenuation of short surface waves by the sea floor via nonlinear sub-harmonic interaction
-
- Published online by Cambridge University Press:
- 08 November 2011, pp. 529-540
-
- Article
- Export citation
- Cited by 14
Vortex formation on a pitching aerofoil at high surging amplitudes
-
- Published online by Cambridge University Press:
- 27 October 2020, A22
-
- Article
- Export citation
- Cited by 14
Morphological instability in a directionally solidifying binary solution with an imposed shear flow
-
- Published online by Cambridge University Press:
- 22 June 2001, pp. 85-106
-
- Article
- Export citation
- Cited by 14
Turbulent wake behind a concave curved cylinder
-
- Published online by Cambridge University Press:
- 18 September 2019, pp. 663-699
-
- Article
- Export citation
- Cited by 14
Nonlinear edge waves and shallow-water theory
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 369-374
-
- Article
- Export citation
- Cited by 14
Passive scalar transport in rotating turbulent channel flow
-
- Published online by Cambridge University Press:
- 04 April 2018, pp. 297-322
-
- Article
- Export citation
- Cited by 14
Turbulence coherence and its impact on wind-farm power fluctuations
-
- Published online by Cambridge University Press:
- 24 September 2018, pp. 1116-1129
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 14
Interactions of a collapsing laser-induced cavitation bubble with a hemispherical droplet attached to a rigid boundary
-
- Published online by Cambridge University Press:
- 28 November 2023, A11
-
- Article
- Export citation
- Cited by 14
Local modulated wave model for the reconstruction of space–time energy spectra in turbulent flows
-
- Published online by Cambridge University Press:
- 14 January 2020, A11
-
- Article
- Export citation
- Cited by 14
Hydrodynamic interaction of two unequal-sized spheres in a slightly rarefied gas: resistance and mobility functions
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 353-378
-
- Article
- Export citation
- Cited by 14
Transitions of flow past a row of square bars
-
- Published online by Cambridge University Press:
- 25 February 2000, pp. 305-323
-
- Article
- Export citation
- Cited by 14
Suspension flow through an asymmetric T-junction
-
- Published online by Cambridge University Press:
- 04 April 2018, pp. 247-273
-
- Article
- Export citation
- Cited by 14
Three-dimensional analysis of precursors to non-viscous dissipation in an experimental turbulent flow
-
- Published online by Cambridge University Press:
- 05 March 2021, A9
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 14
Vortex-induced instabilities and accelerated collapse due to inertial effects of density stratification
-
- Published online by Cambridge University Press:
- 09 February 2010, pp. 415-439
-
- Article
- Export citation
- Cited by 14
The acoustic impedance of a laminar viscous jet through a thin circular aperture
-
- Published online by Cambridge University Press:
- 01 February 2019, pp. 5-44
-
- Article
- Export citation
- Cited by 14
Effects of horizontal pressure gradients on bed destabilization under waves
-
- Published online by Cambridge University Press:
- 05 January 2017, pp. 721-751
-
- Article
- Export citation