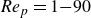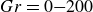Refine search
Actions for selected content:
238 results
Natural convection in a vertical channel. Part 3. Bifurcations of many (additional) unstable periodic orbits and their dynamical relevance
-
- Journal:
- Journal of Fluid Mechanics / Volume 1022 / 10 November 2025
- Published online by Cambridge University Press:
- 05 November 2025, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bifurcation of cellular detonation structure in a mixture with two-stage reactions
-
- Journal:
- Journal of Fluid Mechanics / Volume 1022 / 10 November 2025
- Published online by Cambridge University Press:
- 29 October 2025, A14
-
- Article
- Export citation
Investigating the significance of flatness defects in the origin of hysteresis in flag flutter
-
- Journal:
- Journal of Fluid Mechanics / Volume 1021 / 25 October 2025
- Published online by Cambridge University Press:
- 24 October 2025, A38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spiral vortex flows of the counter-rotating Taylor–Couette system in the narrow-gap limit
-
- Journal:
- Journal of Fluid Mechanics / Volume 1020 / 10 October 2025
- Published online by Cambridge University Press:
- 08 October 2025, A53
-
- Article
- Export citation
Stochastic dynamics of vortex-acoustic lock-in: effects of coloured, multiplicative noise
-
- Journal:
- Journal of Fluid Mechanics / Volume 1020 / 10 October 2025
- Published online by Cambridge University Press:
- 08 October 2025, A55
-
- Article
- Export citation
Nonlinear flapping and symmetry-breaking bifurcation modulation of a piezoelectric metamaterial beam in viscous flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1019 / 25 September 2025
- Published online by Cambridge University Press:
- 18 September 2025, A2
-
- Article
- Export citation
Symmetry groups and invariant solutions of plane Poiseuille flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1019 / 25 September 2025
- Published online by Cambridge University Press:
- 18 September 2025, A36
-
- Article
- Export citation
Bifurcation sequence in the wakes of a sphere and a cube
-
- Journal:
- Journal of Fluid Mechanics / Volume 1018 / 10 September 2025
- Published online by Cambridge University Press:
- 09 September 2025, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Marangoni-flow-driven hysteresis and azimuthal symmetry breaking in evaporating binary droplets
-
- Journal:
- Journal of Fluid Mechanics / Volume 1018 / 10 September 2025
- Published online by Cambridge University Press:
- 29 August 2025, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coupling and synchronisation effects on local lock-in of two thermoacoustic oscillators in a stochastic environment
-
- Journal:
- Journal of Fluid Mechanics / Volume 1017 / 25 August 2025
- Published online by Cambridge University Press:
- 22 August 2025, R2
-
- Article
- Export citation
Analysis of the nonlinear dynamic mechanisms of combustion modes in a rotating detonation combustor
-
- Journal:
- Journal of Fluid Mechanics / Volume 1016 / 10 August 2025
- Published online by Cambridge University Press:
- 08 August 2025, A68
-
- Article
- Export citation
Natural convection of linear entangled polymer in a differentially heated cavity
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 18 July 2025, A32
-
- Article
- Export citation
Stokes waves in rotational flows: internal stagnation and overhanging profiles
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 18 July 2025, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Evaporating sessile droplets: solutal Marangoni effects overwhelm thermal Marangoni flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1013 / 25 June 2025
- Published online by Cambridge University Press:
- 24 June 2025, A39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamic behaviour of a thermal spheroid particle in shear flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 1013 / 25 June 2025
- Published online by Cambridge University Press:
- 23 June 2025, A40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A nonlinear Schrödinger equation for capillary waves on arbitrary depth with constant vorticity
-
- Journal:
- Journal of Fluid Mechanics / Volume 1012 / 10 June 2025
- Published online by Cambridge University Press:
- 09 June 2025, A28
-
- Article
- Export citation
Linear and nonlinear dynamics in radiatively forced cold water
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A24
-
- Article
- Export citation
Dynamics and bifurcations of critical points of vorticity, with application to vortex merging
-
- Journal:
- Journal of Fluid Mechanics / Volume 1010 / 10 May 2025
- Published online by Cambridge University Press:
- 09 May 2025, A64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Three-dimensional coherent structures in a curved pipe flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1007 / 25 March 2025
- Published online by Cambridge University Press:
- 17 March 2025, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear coherent structures in 2-D plane Couette flow with constant throughflow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 03 January 2025, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation