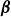Contents
JFM Rapids
Towards a general theory of accelerating foils in the attached-flow regime
-
- Published online by Cambridge University Press:
- 26 May 2025, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A unified framework for mean temperature analysis in compressible turbulent channel flows
-
- Published online by Cambridge University Press:
- 28 May 2025, R2
-
- Article
- Export citation
Revisiting the theory of van Driest: a general scaling law for the skin-friction coefficient of high-speed turbulent boundary layers
-
- Published online by Cambridge University Press:
- 29 May 2025, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measurements of turbulent decay in a von Kármán flow at high Reynolds numbers
-
- Published online by Cambridge University Press:
- 29 May 2025, R4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The effect of shear-thinning on the scalings and small-scale structures of turbulence
-
- Published online by Cambridge University Press:
- 09 June 2025, R5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Focus on Fluids
Drift, diffusion and divergence
-
- Published online by Cambridge University Press:
- 27 May 2025, F1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
The joint effects of planetary
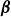 $ \boldsymbol{\beta} $, topography and friction on baroclinic instability in a two-layer quasi-geostrophic model
$ \boldsymbol{\beta} $, topography and friction on baroclinic instability in a two-layer quasi-geostrophic model
-
- Published online by Cambridge University Press:
- 26 May 2025, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Liquid states in horizontal plate-inserted slits
-
- Published online by Cambridge University Press:
- 26 May 2025, A2
-
- Article
- Export citation
Closure dynamics of aortic mechanical heart valves versus bioprosthetic heart valves
-
- Published online by Cambridge University Press:
- 29 May 2025, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scalar transport across the interface between a random sphere pack and a turbulent flow
-
- Published online by Cambridge University Press:
- 28 May 2025, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motion of a rigid sphere penetrating a deep pool
-
- Published online by Cambridge University Press:
- 28 May 2025, A5
-
- Article
- Export citation
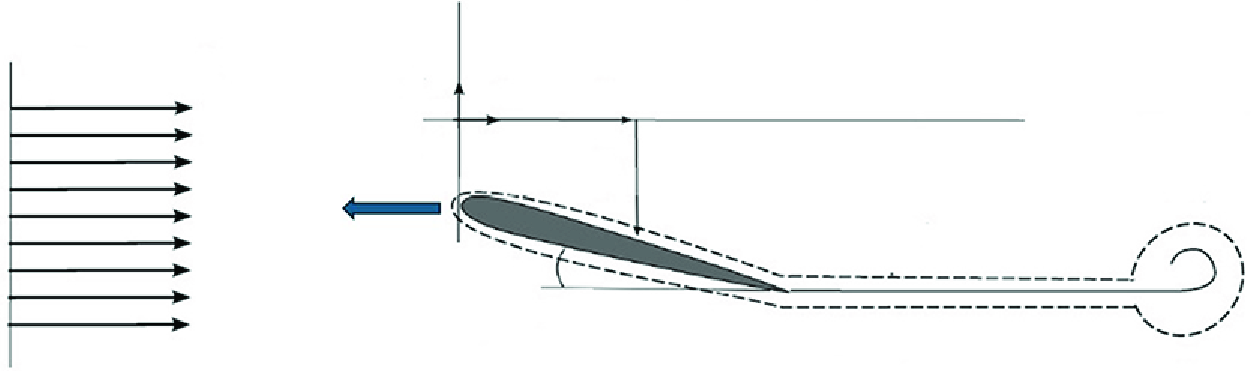
A note on the thrust of airfoils
-
- Published online by Cambridge University Press:
- 29 May 2025, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
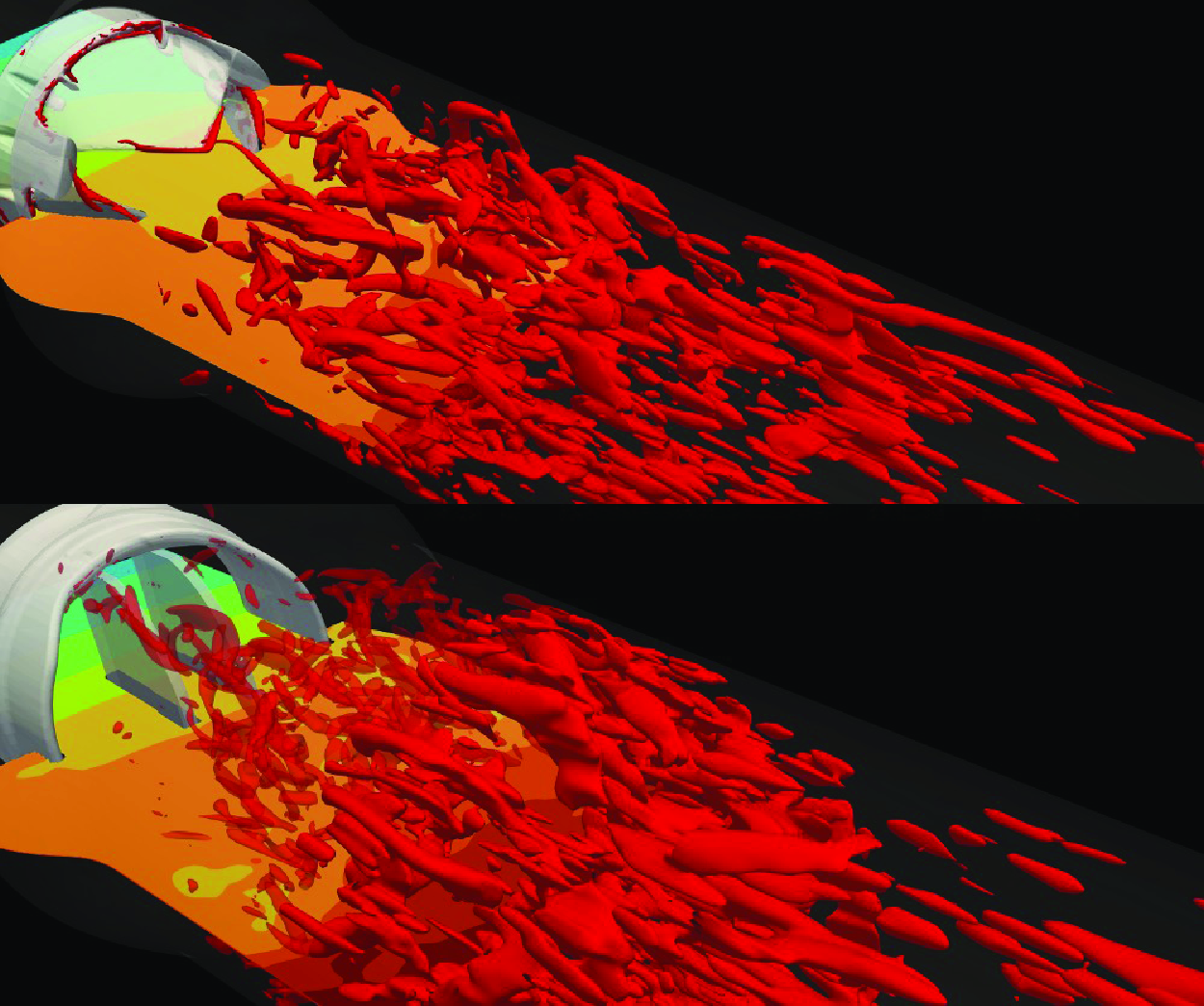
The near-wake vortex dynamics of a wall-mounted hemisphere measured with tomographic particle image velocimetry
-
- Published online by Cambridge University Press:
- 30 May 2025, A7
-
- Article
- Export citation
Reinforcement-learning-assisted control of four-roll mills: geometric symmetry and inertial effect
-
- Published online by Cambridge University Press:
- 02 June 2025, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Molecular streaming in a charged angstrom channel: a toy model
-
- Published online by Cambridge University Press:
- 03 June 2025, A9
-
- Article
- Export citation
Resolvent-based shape optimisation for a two-dimensional cylinder at low Reynolds numbers
-
- Published online by Cambridge University Press:
- 05 June 2025, A10
-
- Article
- Export citation
Acoustothermal effect: mechanism and quantification of the heat source
-
- Published online by Cambridge University Press:
- 04 June 2025, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large deformation of elastic capsules under uniaxial extensional flow
-
- Published online by Cambridge University Press:
- 09 June 2025, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Method of aerodynamic noise source identification for cylinder flows
-
- Published online by Cambridge University Press:
- 04 June 2025, A13
-
- Article
- Export citation
On the formation of a ground vortex in crossflow
-
- Published online by Cambridge University Press:
- 05 June 2025, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation