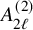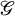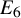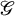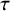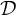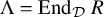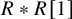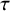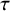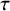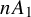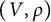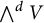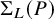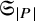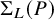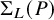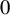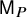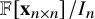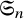Refine search
Actions for selected content:
74 results
Equivariant Ehrhart theory of hypersimplices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 27 October 2025, e178
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Procesi bundle over the Γ-fixed points of the Hilbert scheme of points in
 $\mathbb{C}^2$
$\mathbb{C}^2$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth locus of twisted affine Schubert varieties and twisted affine Demazure modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mutation graph of support
 $\tau $-tilting modules over a skew-gentle algebra
$\tau $-tilting modules over a skew-gentle algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero-one dual characters of flagged Weyl modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 July 2025, pp. 1-23
-
- Article
- Export citation
Orthogonal roots, Macdonald representations, and quasiparabolic sets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 July 2025, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integration on complex Grassmannians, deformed monotone Hurwitz numbers, and interlacing phenomena
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Splines on Cayley graphs of the symmetric group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 June 2025, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gelfand–Tsetlin crystals
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 May 2025, pp. 1-14
-
- Article
- Export citation
Newell–Littlewood numbers III: Eigencones and GIT-semigroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1054-1074
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shuffle formula in science fiction for Macdonald polynomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 28 August 2025, pp. 1075-1127
- Print publication:
- May 2025
-
- Article
- Export citation
A combinatorial formula for the nabla operator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 800-830
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On exterior powers of reflection representations, II
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-23
-
- Article
- Export citation
Kostant’s problem for parabolic Verma modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 594-615
-
- Article
- Export citation
Oriented Temperley–Lieb algebras and combinatorial Kazhdan–Lusztig theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 January 2025, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
0-Hecke modules, domino tableaux, and type-B quasisymmetric functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded Littlewood identity related to alternating sign matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 December 2024, e124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regular Schur labeled skew shape posets and their 0-Hecke modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 November 2024, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Increasing subsequences, matrix loci and Viennot shadows
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An update on Haiman’s conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation