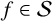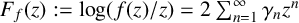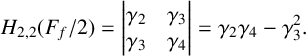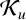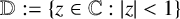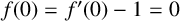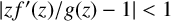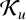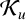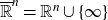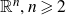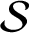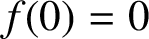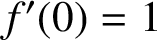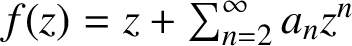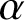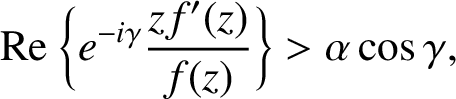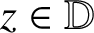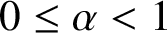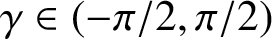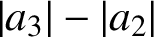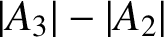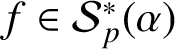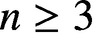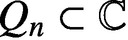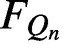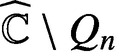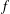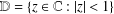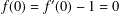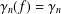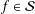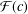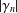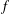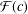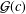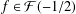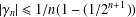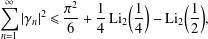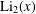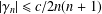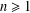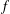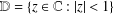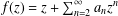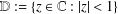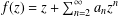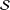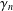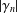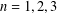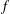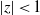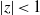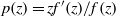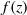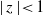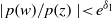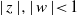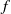Refine search
Actions for selected content:
22 results
THE SHARP BOUND OF THE SECOND HANKEL DETERMINANT OF LOGARITHMIC COEFFICIENTS FOR STARLIKE AND CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 163-171
- Print publication:
- August 2025
-
- Article
- Export citation
SECOND HANKEL DETERMINANT FOR LOGARITHMIC INVERSE COEFFICIENTS OF CONVEX AND STARLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 April 2024, pp. 128-139
- Print publication:
- February 2025
-
- Article
- Export citation
The Schwarzian norm estimates for Janowski convex functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 299-315
-
- Article
- Export citation
ON CERTAIN CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 365-375
- Print publication:
- April 2024
-
- Article
- Export citation
Conformally invariant complete metrics
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 273-300
- Print publication:
- March 2023
-
- Article
- Export citation
A NOTE ON SPIRALLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 25 March 2021, pp. 117-123
- Print publication:
- February 2022
-
- Article
- Export citation
STARLIKENESS AND CONVEXITY OF CAUCHY TRANSFORMS ON REGULAR POLYGONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 291-302
- Print publication:
- April 2021
-
- Article
- Export citation
ON THE DIFFERENCE OF COEFFICIENTS OF OZAKI CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 18 June 2020, pp. 124-131
- Print publication:
- February 2021
-
- Article
- Export citation
ON A CLOSE-TO-CONVEX ANALOGUE OF CERTAIN STARLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 22 January 2020, pp. 268-281
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
LOGARITHMIC COEFFICIENTS PROBLEMS IN FAMILIES RELATED TO STARLIKE AND CONVEX FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 230-249
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
ON OZAKI CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 September 2018, pp. 89-100
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
TOEPLITZ DETERMINANTS WHOSE ELEMENTS ARE THE COEFFICIENTS OF ANALYTIC AND UNIVALENT FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 253-264
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF THE CLUNIE–SHEIL-SMALL THEOREM II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 457-466
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
LOGARITHMIC COEFFICIENTS OF SOME CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 228-237
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
QUASICONFORMAL EXTENSIONS OF HARMONIC MAPPINGS WITH A COMPLEX PARAMETER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 307-315
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF THE CLUNIE–SHEIL-SMALL THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 92-100
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
REMARKS ON THE UNIVALENCE CRITERION OF PASCU AND PASCU
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 210-216
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
UNIVALENCE CRITERIA AND ANALOGUES OF THE JOHN CONSTANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 12 December 2012, pp. 423-434
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
NEIGHBOURHOODS OF UNIVALENT FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 210-219
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
On the logarithmic coefficients of close-to-convex functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-6
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation