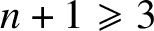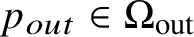Refine search
Actions for selected content:
4 results
Almost global well-posedness for quasilinear strongly coupled wave-Klein-Gordon systems in two space dimensions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 August 2025, e131
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Timelike asymptotics for global solutions to a scalar quasilinear wave equation satisfying the weak null condition
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 July 2025, e108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inverse problems for nonlinear hyperbolic equations with disjoint sources and receivers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 02 November 2021, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GLOBAL NEARLY-PLANE-SYMMETRIC SOLUTIONS TO THE MEMBRANE EQUATION
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 05 August 2020, e13
-
- Article
-
- You have access
- Open access
- Export citation