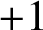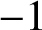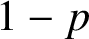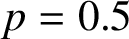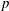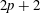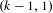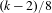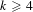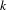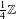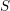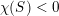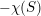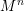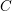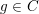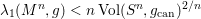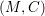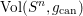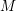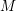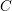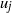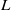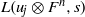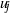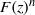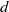Refine search
Actions for selected content:
18 results
Theta functions, fourth moments of eigenforms, and the sup-norm problem I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 03 April 2025, pp. 2916-2969
- Print publication:
- December 2024
-
- Article
- Export citation
A universal inequality for Neumann eigenvalues of the Laplacian on a convex domain in Euclidean space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 19 September 2023, pp. 222-226
- Print publication:
- March 2024
-
- Article
- Export citation
EXTRACTING FEATURES FROM EIGENFUNCTIONS: HIGHER CHEEGER CONSTANTS AND SPARSE EIGENBASIS APPROXIMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 511-512
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
SMALL-SCALE EQUIDISTRIBUTION OF RANDOM WAVES GENERATED BY AN UNFAIR COIN FLIP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 29 November 2021, pp. 222-252
- Print publication:
- April 2023
-
- Article
- Export citation
Inverse problems and rigidity questions in billiard dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 1023-1056
- Print publication:
- March 2022
-
- Article
- Export citation
On the first eigenvalue of the Laplace operator for compact spacelike submanifolds in Lorentz–Minkowski spacetime 𝕃m
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 311-330
- Print publication:
- April 2022
-
- Article
- Export citation
ON NONUNIQUENESS FOR THE ANISOTROPIC CALDERÓN PROBLEM WITH PARTIAL DATA
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 January 2020, e7
-
- Article
-
- You have access
- Open access
- Export citation
The Steklov Problem on Differential Forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 417-435
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
SPECTRAL ANALYSIS OF MORSE–SMALE FLOWS I: CONSTRUCTION OF THE ANISOTROPIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 13 November 2018, pp. 1409-1465
- Print publication:
- September 2020
-
- Article
- Export citation
DYNAMIC ISOPERIMETRY ON GRAPHS AND WEIGHTED RIEMANNIAN MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 514-515
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
EPSTEIN ZETA-FUNCTIONS, SUBCONVEXITY, AND THE PURITY CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 02 April 2018, pp. 581-596
- Print publication:
- March 2020
-
- Article
- Export citation
REDUCTION OF DIMENSION AS A CONSEQUENCE OF NORM-RESOLVENT CONVERGENCE AND APPLICATIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 406-429
- Print publication:
- 2018
-
- Article
- Export citation
Small eigenvalues of surfaces of finite type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 8 / August 2017
- Published online by Cambridge University Press:
- 05 June 2017, pp. 1747-1768
- Print publication:
- August 2017
-
- Article
- Export citation
Spectre et géométrie conforme des variétés compactes à bord
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 28 October 2014, pp. 2112-2126
- Print publication:
- December 2014
-
- Article
- Export citation
DISSOLVING OF CUSP FORMS: HIGHER-ORDER FERMI’S GOLDEN RULES
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 21 January 2013, pp. 269-301
- Print publication:
- July 2013
-
- Article
- Export citation
Hybrid bounds for automorphic forms on ellipsoids over number fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 20 December 2012, pp. 727-758
- Print publication:
- October 2013
-
- Article
- Export citation
BASIC FUNCTIONAL ANALYSIS PUZZLES OF SPECTRAL FLOW
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 19 July 2011, pp. 145-154
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Adiabatic limit of the eta invariant over cofinite quotients of PSL(2, ℝ)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 26 September 2008, pp. 1593-1616
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation