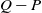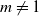Refine search
Actions for selected content:
281 results
A Necessary and Sufficient Condition for the Unique Solution of the Bellman Equation for LTL Surrogate Rewards
-
- Journal:
- Research Directions: Cyber-Physical Systems / Accepted manuscript
- Published online by Cambridge University Press:
- 04 November 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- Export citation
10 - Markov Chains
-
- Book:
- Probability Theory for Quantitative Scientists
- Published online:
- 24 July 2025
- Print publication:
- 14 August 2025, pp 249-288
-
- Chapter
- Export citation
Online matching for the multiclass stochastic block model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1360-1381
- Print publication:
- December 2025
-
- Article
- Export citation
Martingale approach to gambler’s ruin problem for correlated randomwalks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 15 July 2025, pp. 1594-1606
- Print publication:
- December 2025
-
- Article
- Export citation
The replicator coalescent
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1534-1548
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
17 - Coarse-Graining
-
- Book:
- Stochastic Thermodynamics
- Published online:
- 09 June 2025
- Print publication:
- 19 June 2025, pp 324-337
-
- Chapter
- Export citation
Coupling results and Markovian structures for number representations of continuous random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1340-1359
- Print publication:
- December 2025
-
- Article
- Export citation

Markov Chains with Asymptotically Zero Drift
- Lamperti's Problem
-
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025
Hitting times on the lollipop graph
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 4 / October 2025
- Published online by Cambridge University Press:
- 07 March 2025, pp. 486-519
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A non-convex optimization approach of searching algebraic degree phase-type representations for general phase-type distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1101-1137
- Print publication:
- September 2025
-
- Article
- Export citation
An Asymptotic Likelihood Ratio Test for a Markov Chain with Bernoullian or Contingent Input
-
- Journal:
- Psychometrika / Volume 33 / Issue 4 / December 1968
- Published online by Cambridge University Press:
- 01 January 2025, pp. 405-422
-
- Article
- Export citation
The Markov chain embedding problem in a one-jump setting
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 December 2024, pp. 674-696
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUASI-ERGODICITY OF COMPACT STRONG FELLER SEMIGROUPS ON
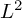 $L^2$
$L^2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 541-584
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Efficiency of reversible MCMC methods: elementary derivations and applications to composite methods
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 188-208
- Print publication:
- March 2025
-
- Article
- Export citation
1 - Topics in representation theory of finite groups
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 1-86
-
- Chapter
- Export citation
29 - Coupled Systems and Diagonalisation
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 334-346
-
- Chapter
- Export citation
(Almost) complete characterization of the stability of a discrete-time Hawkes process with inhibition and memory of length two
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1463-1484
- Print publication:
- December 2024
-
- Article
- Export citation
3 - Markov Chains
- from Part I - Tools and Theory
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 75-116
-
- Chapter
- Export citation
Extreme heat wave sampling and prediction with analog Markov chain and comparisons with deep learning
- Part of
-
- Journal:
- Environmental Data Science / Volume 3 / 2024
- Published online by Cambridge University Press:
- 27 March 2024, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Kolmogorov constant explicit form in the theory of discrete-time stochastic branching systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 04 January 2024, pp. 927-941
- Print publication:
- September 2024
-
- Article
- Export citation























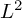
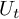
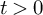
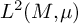
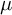
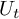
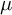
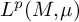
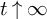
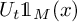 . We discuss several applications and illustrate our results with examples. This includes a complete description of quasi-ergodicity for a large class of semigroups corresponding to non-local Schrödinger operators with confining potentials.
. We discuss several applications and illustrate our results with examples. This includes a complete description of quasi-ergodicity for a large class of semigroups corresponding to non-local Schrödinger operators with confining potentials.