Let (W, S) be a Coxeter system of rank n, and let $p_{(W, S)}(t)$ be its growth function. It is known that $p_{(W, S)}(q^{-1}) \lt \infty$ holds for all $n \leq q \in \mathbb{N}$. In this paper, we will show that this still holds for 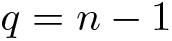$q = n-1$, if (W, S) is 2-spherical. Moreover, we will prove that $p_{(W, S)}(q^{-1}) = \infty$ holds for 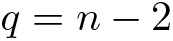$q = n-2$, if the Coxeter diagram of (W, S) is the complete graph. These two results provide a complete characterization of the finiteness of the growth function in the case of 2-spherical Coxeter systems with a complete Coxeter diagram.

We study normal reflection subgroups of complex reflection groups. Our approach leads to a refinement of a theorem of Orlik and Solomon to the effect that the generating function for fixed-space dimension over a reflection group is a product of linear factors involving generalised exponents. Our refinement gives a uniform proof and generalisation of a recent theorem of the second author.

We prove that, under suitable conditions, a Jacobi Poincaré series of exponential type of integer weight and matrix index does not vanish identically. For the classical Jacobi forms, we construct a basis consisting of the ‘first’ few Poincaré series, and also give conditions, both dependent on and independent of the weight, that ensure the nonvanishing of a classical Jacobi Poincaré series. We also obtain a result on the nonvanishing of a Jacobi Poincaré series when an odd prime divides the index.

In this paper we address the issue of existence of cusp forms by using an extension and refinement of a classic method involving (adelic) compactly supported Poincaré series. As a consequence of our adelic approach, we also deal with cusp forms for congruence subgroups.

We break the convexity bound in the t-aspect for L-functions attached to cusp forms f for GL2(k) over arbitrary number fields k. The argument uses asymptotics with error term with a power saving, for second integral moments over spectral families of twists L(s,f⊗χ) by Grossencharacters χ, from our previous paper on integral moments.

We obtain second integral moments of automorphic L-functions on adele groups GL2 over arbitrary number fields, by a spectral decomposition using the structure and representation theory of adele groups GL1 and GL2. This requires reformulation of the notion of Poincaré series, replacing the collection of classical Poincaré series over GL2(ℚ) or GL2(ℚ(i)) with a single, coherent, global object that makes sense over a number field. This is the first expression of integral moments in adele-group terms, distinguishing global and local issues, and allowing uniform application to number fields. When specialized to the field of rational numbers ℚ, we recover the classical results on moments.

We derive upper Gaussian bounds for the heat kernel on complete, noncompact locally symmetric spaces M=Γ∖X with nonpositive curvature. Our bounds contain the Poincaré series of the discrete group Γ and therefore we also provide upper bounds for this series.