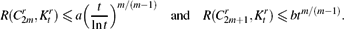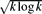Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Induced Turán Numbers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 274-288
-
- Article
- Export citation
New Classes of Degree Sequences with Fast Mixing Swap Markov Chain Sampling
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 186-207
-
- Article
- Export citation
Linear Turán Numbers of Linear Cycles and Cycle-Complete Ramsey Numbers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 358-386
-
- Article
- Export citation

Topics in Computational Number Theory Inspired by Peter L. Montgomery
-
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017
Counting Intersecting and Pairs of Cross-Intersecting Families
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 16 October 2017, pp. 60-68
-
- Article
- Export citation
Monotone Subsequences in High-Dimensional Permutations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 16 October 2017, pp. 69-83
-
- Article
- Export citation
2 - Montgomery Arithmetic from a Software Perspective
-
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp 10-39
-
- Chapter
- Export citation
5 - General Purpose Integer Factoring
-
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp 116-160
-
- Chapter
- Export citation
7 - The Block Lanczos Algorithm
-
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp 175-188
-
- Chapter
- Export citation
3 - Hardware Aspects of Montgomery Modular Multiplication
-
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp 40-81
-
- Chapter
- Export citation
Contents
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp v-x
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp i-iv
-
- Chapter
- Export citation
List of Contributors
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp xi-xii
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp 235-260
-
- Chapter
- Export citation
1 - Introduction
-
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp 1-9
-
- Chapter
- Export citation
Preface
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp xiii-xiv
-
- Chapter
- Export citation
9 - Cryptographic Pairings
-
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp 206-234
-
- Chapter
- Export citation
8 - FFT Extension for Algebraic-Group Factorization Algorithms
-
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp 189-205
-
- Chapter
- Export citation
4 - Montgomery Curves and the Montgomery Ladder
-
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp 82-115
-
- Chapter
- Export citation
Subject Index
-
- Book:
- Topics in Computational Number Theory Inspired by Peter L. Montgomery
- Published online:
- 25 October 2017
- Print publication:
- 12 October 2017, pp 261-266
-
- Chapter
- Export citation