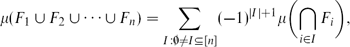Refine search
Actions for selected content:
48284 results in Computer Science
Maximizing the Number of Independent Sets of a Fixed Size
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 3 / May 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 521-527
-
- Article
- Export citation
Simplifying Inclusion–Exclusion Formulas
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 2 / March 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 438-456
-
- Article
- Export citation
‘The Asymptotic Number of Connected d-Uniform Hypergraphs’ — CORRIGENDUM
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 373-375
-
- Article
-
- You have access
- Export citation
Diagonal Asymptotics for Products of Combinatorial Classes
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 10 October 2014, pp. 354-372
-
- Article
- Export citation
Evaluations of Topological Tutte Polynomials
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 3 / May 2015
- Published online by Cambridge University Press:
- 10 October 2014, pp. 556-583
-
- Article
- Export citation
MULTI-ARMED BANDITS UNDER GENERAL DEPRECIATION AND COMMITMENT
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 29 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 10 October 2014, pp. 51-76
-
- Article
-
- You have access
- Export citation
The network structure of mathematical knowledge according to the Wikipedia, MathWorld, and DLMF online libraries
-
- Journal:
- Network Science / Volume 2 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 10 October 2014, pp. 367-386
-
- Article
- Export citation
Preface
-
- Book:
- Thinking Functionally with Haskell
- Published online:
- 05 November 2014
- Print publication:
- 09 October 2014, pp ix-xii
-
- Chapter
- Export citation
1 - What is functional programming?
-
- Book:
- Thinking Functionally with Haskell
- Published online:
- 05 November 2014
- Print publication:
- 09 October 2014, pp 1-21
-
- Chapter
- Export citation
4 - Lists
-
- Book:
- Thinking Functionally with Haskell
- Published online:
- 05 November 2014
- Print publication:
- 09 October 2014, pp 63-88
-
- Chapter
- Export citation
7 - Efficiency
-
- Book:
- Thinking Functionally with Haskell
- Published online:
- 05 November 2014
- Print publication:
- 09 October 2014, pp 145-180
-
- Chapter
- Export citation
Index
-
- Book:
- Thinking Functionally with Haskell
- Published online:
- 05 November 2014
- Print publication:
- 09 October 2014, pp 338-344
-
- Chapter
- Export citation
6 - Proofs
-
- Book:
- Thinking Functionally with Haskell
- Published online:
- 05 November 2014
- Print publication:
- 09 October 2014, pp 110-144
-
- Chapter
- Export citation
2 - Expressions, types and values
-
- Book:
- Thinking Functionally with Haskell
- Published online:
- 05 November 2014
- Print publication:
- 09 October 2014, pp 22-48
-
- Chapter
- Export citation
10 - Imperative functional programming
-
- Book:
- Thinking Functionally with Haskell
- Published online:
- 05 November 2014
- Print publication:
- 09 October 2014, pp 239-275
-
- Chapter
- Export citation
8 - Preety-printing
-
- Book:
- Thinking Functionally with Haskell
- Published online:
- 05 November 2014
- Print publication:
- 09 October 2014, pp 181-209
-
- Chapter
- Export citation
Optimal Codes in the Enomoto-Katona Space
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 2 / March 2015
- Published online by Cambridge University Press:
- 09 October 2014, pp. 382-406
-
- Article
- Export citation
3 - Numbers
-
- Book:
- Thinking Functionally with Haskell
- Published online:
- 05 November 2014
- Print publication:
- 09 October 2014, pp 49-62
-
- Chapter
- Export citation