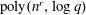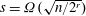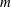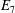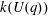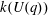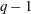Refine search
Actions for selected content:
48287 results in Computer Science
Deterministic polynomial factoring and association schemes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 123-140
-
- Article
-
- You have access
- Export citation
Colouring Planar Graphs With Three Colours and No Large Monochromatic Components
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 551-570
-
- Article
- Export citation
Calculating conjugacy classes in Sylow
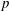 $p$ -subgroups of finite Chevalley groups of rank six and seven
$p$ -subgroups of finite Chevalley groups of rank six and seven
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 109-122
-
- Article
-
- You have access
- Export citation
Bounds for zeros of Meixner and Kravchuk polynomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 47-57
-
- Article
-
- You have access
- Export citation
Implicit self-adjusting computation for purely functional programs
- Part of
-
- Journal:
- Journal of Functional Programming / Volume 24 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 31 March 2014, pp. 56-112
-
- Article
-
- You have access
- Export citation
Randomness in biology
-
- Journal:
- Mathematical Structures in Computer Science / Volume 24 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 28 March 2014, e240308
-
- Article
-
- You have access
- Export citation
Preface to the special issue on developments of the concepts of randomness, statistics and probability
-
- Journal:
- Mathematical Structures in Computer Science / Volume 24 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 28 March 2014, e240301
-
- Article
-
- You have access
- Export citation
Joint distributions, the uncertainty principle and positive distributions†
-
- Journal:
- Mathematical Structures in Computer Science / Volume 24 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 28 March 2014, e240305
-
- Article
- Export citation
Probability, statistics and computation in dynamical systems
-
- Journal:
- Mathematical Structures in Computer Science / Volume 24 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 28 March 2014, e240304
-
- Article
- Export citation
On the concept of probability
-
- Journal:
- Mathematical Structures in Computer Science / Volume 24 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 28 March 2014, e240309
-
- Article
- Export citation
Kolmogorov on the role of randomness in probability theory
-
- Journal:
- Mathematical Structures in Computer Science / Volume 24 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 28 March 2014, e240302
-
- Article
- Export citation
Probability in quantum computation and quantum computational logics: a survey
-
- Journal:
- Mathematical Structures in Computer Science / Volume 24 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 28 March 2014, e240306
-
- Article
- Export citation
Shannon entropy: a rigorous notion at the crossroads between probability, information theory, dynamical systems and statistical physics
-
- Journal:
- Mathematical Structures in Computer Science / Volume 24 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 28 March 2014, e240311
-
- Article
-
- You have access
- Export citation
A quantum random number generator certified by value indefiniteness
-
- Journal:
- Mathematical Structures in Computer Science / Volume 24 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 28 March 2014, e240303
-
- Article
- Export citation