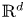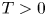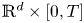Refine search
Actions for selected content:
48202 results in Computer Science
Appendix A: Statistical Techniques
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 367-379
-
- Chapter
- Export citation
Preface
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp xiii-xviii
-
- Chapter
- Export citation
Part III - Unsupervised Learning
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 173-224
-
- Chapter
- Export citation
Appendix F: Connecting with MySQL Databases
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 396-399
-
- Chapter
- Export citation
Contents
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp vii-xii
-
- Chapter
- Export citation
5 - Classification 1
- from Part II - Supervised Learning
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 118-143
-
- Chapter
- Export citation
12 - Designing and Evaluating ML Systems
- from Part V - Further Explorations
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 326-347
-
- Chapter
- Export citation
Part IV - Neural Networks
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 225-300
-
- Chapter
- Export citation
Themes for future research on memory, mind and media
- Part of
-
- Journal:
- Memory, Mind & Media / Volume 1 / 2022
- Published online by Cambridge University Press:
- 29 December 2022, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Appendix E: R for Machine Learning
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 386-395
-
- Chapter
- Export citation
Part II - Supervised Learning
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 79-172
-
- Chapter
- Export citation
13 - Responsible AI
- from Part V - Further Explorations
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 348-366
-
- Chapter
- Export citation
Part V - Further Explorations
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 301-366
-
- Chapter
- Export citation
3 - Cloud Computing
- from Part I - Basic Concepts
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 49-78
-
- Chapter
- Export citation
9 - Neural Networks
- from Part IV - Neural Networks
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 227-263
-
- Chapter
- Export citation
Appendices
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp 367-404
-
- Chapter
- Export citation
Dedication
-
- Book:
- A Hands-On Introduction to Machine Learning
- Published online:
- 20 January 2023
- Print publication:
- 29 December 2022, pp v-vi
-
- Chapter
- Export citation
Asymptotics of a time bounded cylinder model
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 27 December 2022, pp. 1063-1083
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Valuation of vulnerable European options with market liquidity risk
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 65-81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modal FRP for all: Functional reactive programming without space leaks in Haskell
-
- Journal:
- Journal of Functional Programming / Volume 32 / 2022
- Published online by Cambridge University Press:
- 26 December 2022, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation