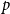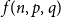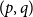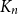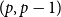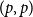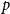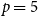Refine search
Actions for selected content:
48287 results in Computer Science
Index
-
- Book:
- Mathematical Logic and Computation
- Published online:
- 08 September 2022
- Print publication:
- 24 November 2022, pp 508-513
-
- Chapter
- Export citation
Index
-
- Book:
- A Comparison Process for Mouse Pairs
- Published online:
- 10 November 2022
- Print publication:
- 24 November 2022, pp 533-536
-
- Chapter
- Export citation
Chapter 9 - Fine Structure for the Least Branch Hierarchy
-
- Book:
- A Comparison Process for Mouse Pairs
- Published online:
- 10 November 2022
- Print publication:
- 24 November 2022, pp 387-440
-
- Chapter
- Export citation
Appendix A - Background
-
- Book:
- Mathematical Logic and Computation
- Published online:
- 08 September 2022
- Print publication:
- 24 November 2022, pp 488-496
-
- Chapter
- Export citation
3 - Semantics of Propositional Logic
-
- Book:
- Mathematical Logic and Computation
- Published online:
- 08 September 2022
- Print publication:
- 24 November 2022, pp 59-82
-
- Chapter
- Export citation
Notation
-
- Book:
- Mathematical Logic and Computation
- Published online:
- 08 September 2022
- Print publication:
- 24 November 2022, pp 504-507
-
- Chapter
- Export citation
GENERALIZED PARTIAL MEET AND KERNEL CONTRACTIONS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 24 November 2022, pp. 366-394
- Print publication:
- June 2024
-
- Article
- Export citation
4 - First-Order Logic
-
- Book:
- Mathematical Logic and Computation
- Published online:
- 08 September 2022
- Print publication:
- 24 November 2022, pp 83-109
-
- Chapter
- Export citation
Preface
-
- Book:
- A Comparison Process for Mouse Pairs
- Published online:
- 10 November 2022
- Print publication:
- 24 November 2022, pp xi-xii
-
- Chapter
- Export citation
1 - Fundamentals
-
- Book:
- Mathematical Logic and Computation
- Published online:
- 08 September 2022
- Print publication:
- 24 November 2022, pp 1-27
-
- Chapter
- Export citation
New upper bounds for the Erdős-Gyárfás problem on generalized Ramsey numbers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 24 November 2022, pp. 349-362
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
15 - Second-Order Logic and Arithmetic
-
- Book:
- Mathematical Logic and Computation
- Published online:
- 08 September 2022
- Print publication:
- 24 November 2022, pp 409-439
-
- Chapter
- Export citation
Preface
-
- Book:
- Mathematical Logic and Computation
- Published online:
- 08 September 2022
- Print publication:
- 24 November 2022, pp ix-xi
-
- Chapter
- Export citation
Efficiently generating geometric inhomogeneous and hyperbolic random graphs
-
- Journal:
- Network Science / Volume 10 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 23 November 2022, pp. 361-380
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NLE volume 28 issue 6 Cover and Back matter
-
- Journal:
- Natural Language Engineering / Volume 28 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 23 November 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation
A dual-context sequent calculus for the constructive modal logic S4
-
- Journal:
- Mathematical Structures in Computer Science / Volume 32 / Issue 9 / October 2022
- Published online by Cambridge University Press:
- 23 November 2022, pp. 1205-1233
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NLE volume 28 issue 6 Cover and Front matter
-
- Journal:
- Natural Language Engineering / Volume 28 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 23 November 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Is the Capabilities Approach operationalizable to analyse the impact of digital identity on human lives
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 23 November 2022, e43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Understanding collaboration patterns on funded research projects: A network analysis
-
- Journal:
- Network Science / Volume 11 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 143-173
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

The E-Primer
- An Introduction to Creating Psychological Experiments in E-Prime
-
- Published by:
- Amsterdam University Press
- Published online:
- 22 November 2022
- Print publication:
- 04 March 2019
-
- Book
- Export citation