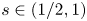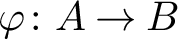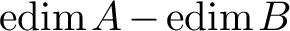Refine search
Actions for selected content:
25845 results in Abstract analysis
Periodic solutions for one-dimensional nonlinear nonlocal problem with drift including singular nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 23 December 2021, pp. 229-261
- Print publication:
- February 2023
-
- Article
- Export citation
A FREENESS CRITERION WITHOUT PATCHING FOR MODULES OVER LOCAL RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 20 December 2021, pp. 2117-2129
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Series expansion of Leray–Trudinger inequality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 20 December 2021, pp. 262-274
- Print publication:
- February 2023
-
- Article
- Export citation
Index estimates for closed minimal submanifolds of the sphere
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 December 2021, pp. 802-816
- Print publication:
- June 2022
-
- Article
- Export citation
Optimal Hardy-weights for the (p, A)-Laplacian with a potential term
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 17 December 2021, pp. 289-306
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Frontmatter
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp i-iv
-
- Chapter
- Export citation
2 - Formal Reproducing Kernel Hilbert Spaces
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 26-41
-
- Chapter
- Export citation
Contents
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp v-viii
-
- Chapter
- Export citation
9 - Weighted Hardy–Fock Spaces Built from a Regular Formal Power Series
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 315-414
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp x-x
-
- Chapter
- Export citation
Inverse nodal problems on quantum tree graphs
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 16 December 2021, pp. 275-288
- Print publication:
- February 2023
-
- Article
- Export citation
4 - Stein Relations and Observability Range Spaces
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 103-179
-
- Chapter
- Export citation
Notation Index
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 425-426
-
- Chapter
- Export citation
3 - Contractive Multipliers
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 42-102
-
- Chapter
- Export citation
6 - Non-orthogonal Beurling–Lax Representations Based on Wandering Subspaces
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 215-229
-
- Chapter
- Export citation
Subject Index
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 427-428
-
- Chapter
- Export citation
The fragmentation equation with size diffusion: Well posedness and long-term behaviour
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 16 December 2021, pp. 1083-1116
-
- Article
- Export citation
7 - Orthogonal Beurling–Lax Representations Based on Wandering Subspaces
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 230-284
-
- Chapter
- Export citation
Preface
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp ix-ix
-
- Chapter
- Export citation
8 - Models for ω-Hypercontractive Operator Tuples
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 285-314
-
- Chapter
- Export citation