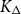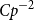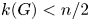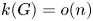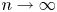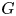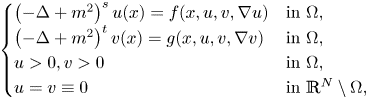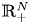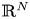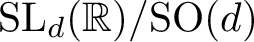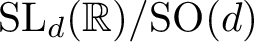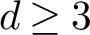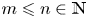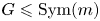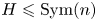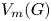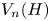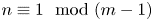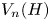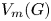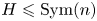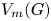Refine search
Actions for selected content:
25847 results in Abstract analysis
Preface
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp ix-ix
-
- Chapter
- Export citation
8 - Models for ω-Hypercontractive Operator Tuples
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 285-314
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 1-27
-
- Chapter
- Export citation
5 - Beurling–Lax Theorems Based on Contractive Multipliers
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 180-214
-
- Chapter
- Export citation
References
-
- Book:
- Noncommutative Function-Theoretic Operator Theory and Applications
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021, pp 415-424
-
- Chapter
- Export citation
Tuning as convex optimisation: a polynomial tuner for multi-parametric combinatorial samplers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 15 December 2021, pp. 765-811
-
- Article
- Export citation
A spanning bandwidth theorem in random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 598-628
-
- Article
- Export citation
A characterization of alternating links in thickened surfaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 December 2021, pp. 177-195
- Print publication:
- February 2023
-
- Article
- Export citation
On the number of conjugacy classes of a primitive permutation group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 December 2021, pp. 115-136
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Liouville-type results for positive solutions of pseudo-relativistic Schrödinger system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 December 2021, pp. 196-228
- Print publication:
- February 2023
-
- Article
- Export citation
QUANTUM ERGODICITY FOR COMPACT QUOTIENTS OF
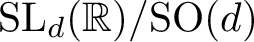 $\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$ IN THE BENJAMINI–SCHRAMM LIMIT
$\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$ IN THE BENJAMINI–SCHRAMM LIMIT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 13 December 2021, pp. 2075-2115
- Print publication:
- September 2023
-
- Article
- Export citation
Spreading speeds and traveling wave solutions of diffusive vector-borne disease models without monotonicity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 December 2021, pp. 137-166
- Print publication:
- February 2023
-
- Article
- Export citation
Cut cotorsion pairs
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 December 2021, pp. 548-585
-
- Article
- Export citation

Noncommutative Function-Theoretic Operator Theory and Applications
-
- Published online:
- 09 December 2021
- Print publication:
- 16 December 2021
PEM series 2 volume 64 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 09 December 2021, pp. b1-b2
-
- Article
-
- You have access
- Export citation
PEM series 2 volume 64 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 09 December 2021, pp. f1-f2
-
- Article
-
- You have access
- Export citation
GMJ volume 64 issue 1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Exact solutions and critical behaviour for a linear growth-diffusion equation on a time-dependent domain
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. 53-79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GMJ volume 64 issue 1 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Some embeddings between symmetric R. thompson groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. 1-18
-
- Article
- Export citation