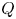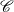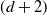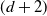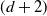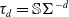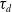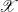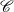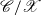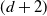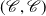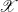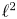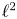Refine search
Actions for selected content:
25845 results in Abstract analysis
JMJ volume 20 Issue 6 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 29 October 2021, pp. f1-f2
- Print publication:
- November 2021
-
- Article
-
- You have access
- Export citation
The Tutte polynomial and toric Nakajima quiver varieties
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 27 October 2021, pp. 1323-1339
- Print publication:
- October 2022
-
- Article
- Export citation
Higher-dimensional Auslander–Reiten theory on (d+2)-angulated categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 October 2021, pp. 527-547
-
- Article
- Export citation
Free quotients of fundamental groups of smooth quasi-projective varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 27 October 2021, pp. 924-946
-
- Article
- Export citation
Tilting pairs in extriangulated categories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 26 October 2021, pp. 947-981
-
- Article
- Export citation
The first $\ell ^{2}$
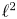 -betti number and groups acting on trees
-betti number and groups acting on trees
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 25 October 2021, pp. 916-923
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extending the Tutte and Bollobás–Riordan polynomials to rank 3 weakly coloured stranded graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 25 October 2021, pp. 507-549
-
- Article
- Export citation
PEM series 2 volume 64 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 25 October 2021, pp. f1-f2
-
- Article
-
- You have access
- Export citation
The wigner property for CL-spaces and finite-dimensional polyhedral banach spaces – RETRACTION
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 25 October 2021, p. 716
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PEM series 2 volume 64 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 25 October 2021, pp. b1-b2
-
- Article
-
- You have access
- Export citation
TRANSITION DENSITIES OF SUBORDINATORS OF POSITIVE ORDER
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 22 October 2021, pp. 1119-1179
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Preface
-
- Book:
- Orthogonal Polynomials in the Spectral Analysis of Markov Processes
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp ix-xii
-
- Chapter
- Export citation
References
-
- Book:
- Orthogonal Polynomials in the Spectral Analysis of Markov Processes
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp 322-330
-
- Chapter
- Export citation
1 - Spectral Representation of Discrete-Time Birth–Death Chains
-
- Book:
- Orthogonal Polynomials in the Spectral Analysis of Markov Processes
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp 1-56
-
- Chapter
- Export citation
2 - Small Phenomena, Big Implications
-
- Book:
- Orthogonal Polynomials in the Spectral Analysis of Markov Processes
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp 57-145
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Orthogonal Polynomials in the Spectral Analysis of Markov Processes
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp i-iv
-
- Chapter
- Export citation
Contents
-
- Book:
- Orthogonal Polynomials in the Spectral Analysis of Markov Processes
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp vii-viii
-
- Chapter
- Export citation
4 - Spectral Representation of Diffusion Processes
-
- Book:
- Orthogonal Polynomials in the Spectral Analysis of Markov Processes
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp 254-321
-
- Chapter
- Export citation
3 - Spectral Representation of Birth–Death Processes
-
- Book:
- Orthogonal Polynomials in the Spectral Analysis of Markov Processes
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp 146-253
-
- Chapter
- Export citation
Dedication
-
- Book:
- Orthogonal Polynomials in the Spectral Analysis of Markov Processes
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp v-vi
-
- Chapter
- Export citation