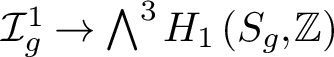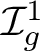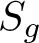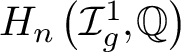Refine search
Actions for selected content:
25845 results in Abstract analysis
Index
-
- Book:
- Orthogonal Polynomials in the Spectral Analysis of Markov Processes
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp 331-334
-
- Chapter
- Export citation
Charge transport modelling of Lithium-ion batteries
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 21 October 2021, pp. 983-1031
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Expansions for the linear-elastic contribution to the self-interaction force of dislocation curves
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 20 October 2021, pp. 1032-1061
-
- Article
- Export citation
Asymptotics for the number of standard tableaux of skew shape and for weighted lozenge tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 550-573
-
- Article
- Export citation
ABELIAN CYCLES IN THE HOMOLOGY OF THE TORELLI GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1703-1726
- Print publication:
- July 2023
-
- Article
- Export citation
AUTOMORPHIC LEFSCHETZ PROPERTIES FOR NONCOMPACT ARITHMETIC MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1655-1702
- Print publication:
- July 2023
-
- Article
- Export citation
AN APERIODIC TILE WITH EDGE-TO-EDGE ORIENTATIONAL MATCHING RULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1727-1755
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
20 - Many Servers with Abandonment
- from Part VI - Many-Server Systems
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 346-359
-
- Chapter
- Export citation
12 - Processing Networks and Maximum Pressure Policies
- from Part IV - Fluid Models of Multi-Class Queueing
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 197-218
-
- Chapter
- Export citation
4 - The G/G/1 Queue
- from Part II - Approximations of the Single Queue
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 61-70
-
- Chapter
- Export citation
8 - Product-Form Queueing Networks
- from Part III - Queueing Networks
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 125-142
-
- Chapter
- Export citation
18 - Infinite Servers Revisited
- from Part VI - Many-Server Systems
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 323-329
-
- Chapter
- Export citation
Part VI - Many-Server Systems
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 321-322
-
- Chapter
- Export citation
9 - Generalized Jackson Networks
- from Part III - Queueing Networks
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 143-156
-
- Chapter
- Export citation
16 - Control in Balanced Heavy Traffic
- from Part V - Diffusion Scaled Balanced Heavy Traffic
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 270-304
-
- Chapter
- Export citation
CONGRUENCES OF SAITO–KUROKAWA LIFTS AND DENOMINATORS OF CENTRAL SPINOR L-VALUES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 14 October 2021, pp. 504-525
-
- Article
- Export citation
22 - Parallel Servers with Skill-Based Routing
- from Part VI - Many-Server Systems
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 385-412
-
- Chapter
- Export citation
11 - Stability of MCQN via Fluid Limits
- from Part IV - Fluid Models of Multi-Class Queueing
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 175-196
-
- Chapter
- Export citation
7 - Diffusions and Brownian Processes
- from Part II - Approximations of the Single Queue
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 102-122
-
- Chapter
- Export citation
13 - Processing Networks with Infinite Virtual Queues
- from Part IV - Fluid Models of Multi-Class Queueing
-
- Book:
- Scheduling and Control of Queueing Networks
- Published online:
- 01 October 2021
- Print publication:
- 14 October 2021, pp 219-235
-
- Chapter
- Export citation