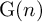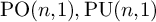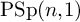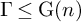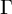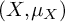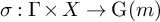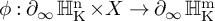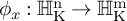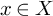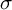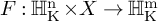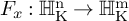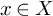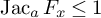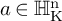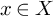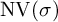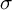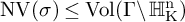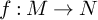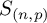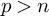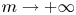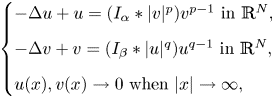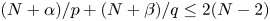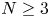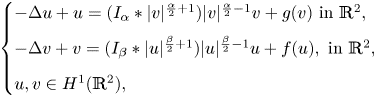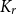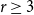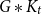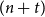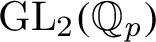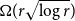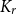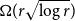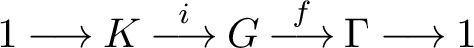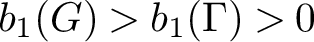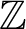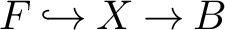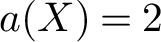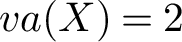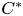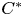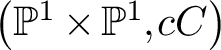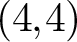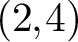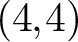Refine search
Actions for selected content:
25845 results in Abstract analysis
NATURAL MAPS FOR MEASURABLE COCYCLES OF COMPACT HYPERBOLIC MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 421-448
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE p-ZASSENHAUS FILTRATION OF A FREE PROFINITE GROUP AND SHUFFLE RELATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 961-983
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behaviour of positive solutions of semilinear elliptic problems with increasing powers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 28 September 2021, pp. 1233-1250
- Print publication:
- October 2022
-
- Article
- Export citation
KHOVANOV SPECTRA FOR TANGLES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 28 September 2021, pp. 1509-1580
- Print publication:
- July 2023
-
- Article
- Export citation
Expansion for the critical point of site percolation: the first three terms
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 28 September 2021, pp. 430-454
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence and nonexistence results for a class of Hamiltonian Choquard-type elliptic systems with lower critical growth on ℝ2
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 28 September 2021, pp. 1383-1410
- Print publication:
- December 2022
-
- Article
- Export citation
ORDERS OF GROWTH AND GENERALIZED ENTROPY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 28 September 2021, pp. 1581-1613
- Print publication:
- July 2023
-
- Article
- Export citation
On deficiency problems for graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 478-488
-
- Article
- Export citation
ON SOME CONSEQUENCES OF A THEOREM OF J. LUDWIG
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1067-1106
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Strong complete minors in digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 24 September 2021, pp. 489-506
-
- Article
- Export citation
Benson's cofibrants, Gorenstein projectives and a related conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 23 September 2021, pp. 779-799
-
- Article
- Export citation
The Fokker–Planck equation for the time-changed fractional Ornstein–Uhlenbeck stochastic process
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 1032-1057
- Print publication:
- August 2022
-
- Article
- Export citation
BNS INVARIANTS AND ALGEBRAIC FIBRATIONS OF GROUP EXTENSIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 21 September 2021, pp. 985-999
- Print publication:
- March 2023
-
- Article
- Export citation
Well-posedness of the free surface problem on a Newtonian fluid between cylinders rotating at different speeds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 1251-1276
- Print publication:
- October 2022
-
- Article
- Export citation
Global regularity criterion for the dissipative systems modelling electrohydrodynamics involving the middle eigenvalue of the strain tensor
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 1277-1290
- Print publication:
- October 2022
-
- Article
- Export citation
Invariance of KMS states on graph C*-algebras under classical and quantum symmetry
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 20 September 2021, pp. 762-778
-
- Article
- Export citation
CORRIGENDUM TO: A FAST ALGORITHM FOR CALCULATING S-INVARIANTS
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 20 September 2021, p. 526
-
- Article
-
- You have access
- Export citation
PRM volume 151 issue 5 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 17 September 2021, pp. b1-b2
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
PRM volume 151 issue 5 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 17 September 2021, pp. f1-f2
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
K-MODULI OF CURVES ON A QUADRIC SURFACE AND K3 SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 16 September 2021, pp. 1251-1291
- Print publication:
- May 2023
-
- Article
- Export citation