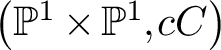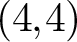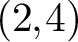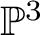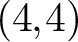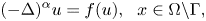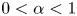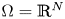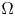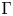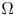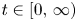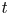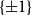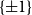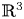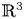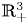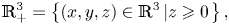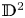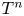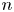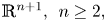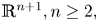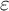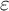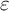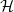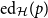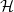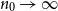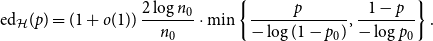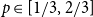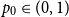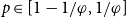Refine search
Actions for selected content:
25847 results in Abstract analysis
PRM volume 151 issue 5 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 17 September 2021, pp. f1-f2
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
K-MODULI OF CURVES ON A QUADRIC SURFACE AND K3 SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 16 September 2021, pp. 1251-1291
- Print publication:
- May 2023
-
- Article
- Export citation
Qualitative properties of singular solutions to fractional elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 14 September 2021, pp. 1155-1190
- Print publication:
- October 2022
-
- Article
- Export citation
On the number of Hadamard matrices via anti-concentration
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 10 September 2021, pp. 455-477
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigid centres on the center manifold of tridimensional differential systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 07 September 2021, pp. 1058-1080
- Print publication:
- August 2022
-
- Article
- Export citation
On the Cauchy problem associated with the Brinkman flow in
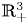 $\mathbb {R}_{+}^{3}$
$\mathbb {R}_{+}^{3}$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 07 September 2021, pp. 1089-1108
- Print publication:
- October 2022
-
- Article
- Export citation
EJAM Editorial: 30th Anniversary Special Issue
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 06 September 2021, pp. 747-748
-
- Article
-
- You have access
- Export citation
Riemannian approximation in Carnot groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 1139-1154
- Print publication:
- October 2022
-
- Article
- Export citation
Discs area-minimizing in mean convex Riemannian n-manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 1361-1382
- Print publication:
- December 2022
-
- Article
- Export citation
On regular algebraic hypersurfaces with non-zero constant mean curvature in Euclidean spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 1081-1088
- Print publication:
- August 2022
-
- Article
- Export citation
GEOMETRIC LOCAL
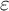 $\varepsilon $-FACTORS IN HIGHER DIMENSIONS
$\varepsilon $-FACTORS IN HIGHER DIMENSIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 02 September 2021, pp. 1887-1913
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
On the edit distance function of the random graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 02 September 2021, pp. 345-367
-
- Article
- Export citation
JMJ volume 20 Issue 5 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 13 September 2021, pp. f1-f2
- Print publication:
- September 2021
-
- Article
-
- You have access
- Export citation
JMJ volume 20 Issue 5 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 13 September 2021, pp. b1-b2
- Print publication:
- September 2021
-
- Article
-
- You have access
- Export citation
10 - Linear Differential Equations
-
- Book:
- A Course of Modern Analysis
- Published online:
- 07 August 2021
- Print publication:
- 26 August 2021, pp 201-218
-
- Chapter
- Export citation
8 - Asymptotic Expansions and Summable Series
-
- Book:
- A Course of Modern Analysis
- Published online:
- 07 August 2021
- Print publication:
- 26 August 2021, pp 153-162
-
- Chapter
- Export citation
9 - Fourier Series and Trigonometric Series
-
- Book:
- A Course of Modern Analysis
- Published online:
- 07 August 2021
- Print publication:
- 26 August 2021, pp 163-200
-
- Chapter
- Export citation
14 - The Hypergeometric Function
-
- Book:
- A Course of Modern Analysis
- Published online:
- 07 August 2021
- Print publication:
- 26 August 2021, pp 293-315
-
- Chapter
- Export citation
Computing the fundamental group of a higher-rank graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 26 August 2021, pp. 650-661
-
- Article
- Export citation
3 - Continuous Functions and Uniform Convergence
-
- Book:
- A Course of Modern Analysis
- Published online:
- 07 August 2021
- Print publication:
- 26 August 2021, pp 40-57
-
- Chapter
- Export citation