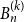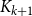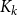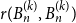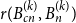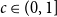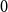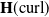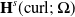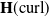Search results for Abstract analysis

Off-diagonal book Ramsey numbers
Part of
- Graph theory
- Extremal combinatorics
David Conlon, Jacob Fox, Yuval Wigderson
Journal:

Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023

Published online by Cambridge University Press:

09 January 2023, pp. 516-545
- Article
- - You have access
  - Open access
- PDF
- HTML
- Export citation
The book graph $B_n ^{(k)}$ consists of $n$ copies of $K_{k+1}$ joined along a common $K_k$. In the prequel to this paper, we studied the diagonal Ramsey number $r(B_n ^{(k)}, B_n ^{(k)})$. Here we consider the natural off-diagonal variant $r(B_{cn} ^{(k)}, B_n^{(k)})$ for fixed $c \in (0,1]$. In this more general setting, we show that an interesting dichotomy emerges: for very small $c$, a simple $k$-partite construction dictates the Ramsey function and all nearly-extremal colourings are close to being $k$-partite, while, for $c$ bounded away from $0$, random colourings of an appropriate density are asymptotically optimal and all nearly-extremal colourings are quasirandom. Our investigations also open up a range of questions about what happens for intermediate values of $c$.

15 - Open Problems and Related Topics
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 326-331
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

Foreword
- By András Vasy
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp xi-xiv
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

Solving two-dimensional H(curl)-elliptic interface systems with optimal convergence on unfitted meshes
Part of
- Partial differential equations, boundary value problems
- Miscellaneous topics - Partial differential equations
Ruchi Guo, Yanping Lin, Jun Zou
Journal:

European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023

Published online by Cambridge University Press:

05 January 2023, pp. 774-805
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
Finite element methods developed for unfitted meshes have been widely applied to various interface problems. However, many of them resort to non-conforming spaces for approximation, which is a critical obstacle for the extension to $\textbf{H}(\text{curl})$ equations. This essential issue stems from the underlying Sobolev space $\textbf{H}^s(\text{curl};\,\Omega)$, and even the widely used penalty methodology may not yield the optimal convergence rate. One promising approach to circumvent this issue is to use a conforming test function space, which motivates us to develop a Petrov–Galerkin immersed finite element (PG-IFE) method for $\textbf{H}(\text{curl})$-elliptic interface problems. We establish the Nédélec-type IFE spaces and develop some important properties including their edge degrees of freedom, an exact sequence relating to the $H^1$ IFE space and optimal approximation capabilities. We analyse the inf-sup condition under certain assumptions and show the optimal convergence rate, which is also validated by numerical experiments.

12 - The Attenuated Geodesic X-ray Transform
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 269-276
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

Index
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 342-344
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

10 - Tensor Tomography
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 233-240
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

4 - The Geodesic X-ray Transform
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 107-129
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

Preface
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp xv-xxii
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

13 - Non-Abelian X-ray Transforms
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 277-303
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

8 - Microlocal Aspects, Surjectivity of I0*
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 189-207
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

2 - Radial Sound Speeds
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 25-51
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

9 - Inversion Formulas and Range
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 208-232
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

Dedication
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp v-vi
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

7 - The X-ray Transform in Non-positive Curvature
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 171-188
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

References
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 332-341
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

Frontmatter
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp i-iv
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

Contents
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp vii-x
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

1 - The Radon Transform in the Plane
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 1-24
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

3 - Geometric Preliminaries
Gabriel P. Paternain, University of Cambridge, Mikko Salo, University of Jyväskylä, Finland, Gunther Uhlmann, University of Washington
Book:

Geometric Inverse Problems

Published online:

15 January 2023

Print publication:

05 January 2023, pp 52-106
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation

Abstract analysis

Refine search

Refine search

Actions for selected content:

25820 results in Abstract analysis

Off-diagonal book Ramsey numbers

15 - Open Problems and Related Topics

Foreword

Solving two-dimensional H(curl)-elliptic interface systems with optimal convergence on unfitted meshes

12 - The Attenuated Geodesic X-ray Transform

Index

10 - Tensor Tomography

4 - The Geodesic X-ray Transform

Preface

13 - Non-Abelian X-ray Transforms

8 - Microlocal Aspects, Surjectivity of I0*

2 - Radial Sound Speeds

9 - Inversion Formulas and Range

Dedication

7 - The X-ray Transform in Non-positive Curvature

References

Frontmatter

Contents

1 - The Radon Transform in the Plane

3 - Geometric Preliminaries

Abstract analysis

Refine search

Refine search

Actions for selected content:

Save Search

25820 results in Abstract analysis