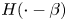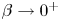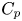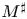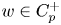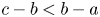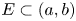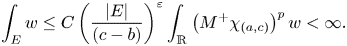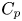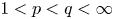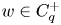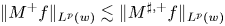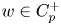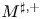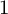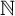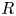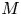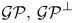Refine search
Actions for selected content:
25820 results in Abstract analysis
Acknowledgements
-
- Book:
- Geometric Inverse Problems
- Published online:
- 15 January 2023
- Print publication:
- 05 January 2023, pp xxiii-xxiv
-
- Chapter
- Export citation
5 - Regularity Results for the Transport Equation
-
- Book:
- Geometric Inverse Problems
- Published online:
- 15 January 2023
- Print publication:
- 05 January 2023, pp 130-141
-
- Chapter
- Export citation
14 - Non-Abelian X-ray Transforms II
-
- Book:
- Geometric Inverse Problems
- Published online:
- 15 January 2023
- Print publication:
- 05 January 2023, pp 304-325
-
- Chapter
- Export citation
11 - Boundary Rigidity
-
- Book:
- Geometric Inverse Problems
- Published online:
- 15 January 2023
- Print publication:
- 05 January 2023, pp 241-268
-
- Chapter
- Export citation
6 - Vertical Fourier Analysis
-
- Book:
- Geometric Inverse Problems
- Published online:
- 15 January 2023
- Print publication:
- 05 January 2023, pp 142-170
-
- Chapter
- Export citation
JMJ volume 22 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. f1-f2
- Print publication:
- January 2023
-
- Article
-
- You have access
- Export citation
JMJ volume 22 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. b1-b2
- Print publication:
- January 2023
-
- Article
-
- You have access
- Export citation
On a quasilinear elliptic problem involving the 1-Laplacian operator and a discontinuous nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 28 December 2022, pp. 33-59
- Print publication:
- February 2024
-
- Article
- Export citation
One-sided $C_{p}$
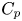 estimates via $M^{\sharp }$
estimates via $M^{\sharp }$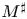 function
function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 27 December 2022, pp. 2079-2105
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRUCTURAL STABILITY OF MEANDERING-HYPERBOLIC GROUP ACTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 753-810
- Print publication:
- March 2024
-
- Article
- Export citation
BANACH SPACES IN WHICH LARGE SUBSETS OF SPHERES CONCENTRATE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 737-752
- Print publication:
- March 2024
-
- Article
- Export citation
FP-injective dimensions and Gorenstein homology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 21 December 2022, pp. 1183-1199
-
- Article
- Export citation
Pointwise Assouad dimension for measures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 21 December 2022, pp. 2053-2078
- Print publication:
- December 2023
-
- Article
- Export citation
Two approximate symmetry frameworks for nonlinear partial differential equations with a small parameter: Comparisons, relations, approximate solutions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 16 December 2022, pp. 1017-1045
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
References
-
- Book:
- Exponential Families in Theory and Practice
- Published online:
- 25 November 2022
- Print publication:
- 15 December 2022, pp 239-242
-
- Chapter
- Export citation
3 - Generalized Linear Models
-
- Book:
- Exponential Families in Theory and Practice
- Published online:
- 25 November 2022
- Print publication:
- 15 December 2022, pp 88-140
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Exponential Families in Theory and Practice
- Published online:
- 25 November 2022
- Print publication:
- 15 December 2022, pp i-iv
-
- Chapter
- Export citation
Introduction
-
- Book:
- Exponential Families in Theory and Practice
- Published online:
- 25 November 2022
- Print publication:
- 15 December 2022, pp xi-xii
-
- Chapter
- Export citation
Preface
-
- Book:
- Exponential Families in Theory and Practice
- Published online:
- 25 November 2022
- Print publication:
- 15 December 2022, pp vii-viii
-
- Chapter
- Export citation
4 - Curved Exponential Families, Empirical Bayes, Missing Data, and Stability of the MLE
-
- Book:
- Exponential Families in Theory and Practice
- Published online:
- 25 November 2022
- Print publication:
- 15 December 2022, pp 141-182
-
- Chapter
- Export citation