Refine search
Actions for selected content:
2584 results in Computational Science
2 - Modular arithmetic and the FFT
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp 47-78
-
- Chapter
- Export citation
4 - Elementary and special function evaluation
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp 125-184
-
- Chapter
- Export citation
Notation
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp xiii-xvi
-
- Chapter
- Export citation
The yoga of the Cassels–Tate pairing
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 November 2010, pp. 451-460
-
- Article
-
- You have access
- Export citation
Points of low height on elliptic surfaces with torsion
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 27 August 2010, pp. 370-387
-
- Article
-
- You have access
- Export citation
The Alperin weight conjecture and Uno’s conjecture for the Monster 𝕄, p odd
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 27 August 2010, pp. 320-356
-
- Article
-
- You have access
- Export citation

Exact and Approximate Controllability for Distributed Parameter Systems
- A Numerical Approach
-
- Published online:
- 04 August 2010
- Print publication:
- 20 March 2008
Perfect posterior simulation for mixture and hidden Markov models
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 246-259
-
- Article
-
- You have access
- Export citation
Normalizers of 2-subgroups in black-box groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 307-319
-
- Article
-
- You have access
- Export citation
Approximating the Schur multiplier of certain infinitely presented groups via nilpotent quotients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 260-271
-
- Article
-
- You have access
- Export citation
On 1-dimensional representations of finite W-algebras associated to simple Lie algebras of exceptional type
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 357-369
-
- Article
-
- You have access
- Export citation
Constructing representations of Hecke algebras for complex reflection groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 426-450
-
- Article
-
- You have access
- Export citation
The complexity of the four colour theorem
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 414-425
-
- Article
-
- You have access
- Export citation
The Mordell–Weil sieve: proving non-existence of rational points on curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 272-306
-
- Article
-
- You have access
- Export citation
The minimal density of triangles in tripartite graphs
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 388-413
-
- Article
-
- You have access
- Export citation
Application of the Kusuoka approximation with a tree-based branching algorithm to the pricing of interest-rate derivatives under the HJM model
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 July 2010, pp. 208-221
-
- Article
-
- You have access
- Export citation
Fundamental domains for genus-zero and genus-one congruence subgroups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 July 2010, pp. 222-245
-
- Article
-
- You have access
- Export citation
Explicit computations of Serre’s obstruction for genus-3 curves and application to optimal curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 192-207
-
- Article
-
- You have access
- Export citation
Constructing maximal subgroups of orthogonal groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 164-191
-
- Article
-
- You have access
- Export citation
An extension of Buchberger’s criteria for Gröbner basis decision
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 111-129
-
- Article
-
- You have access
- Export citation
 for a non-torsion point
for a non-torsion point 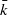 , being a Jacobian over
, being a Jacobian over 