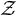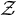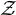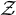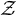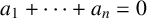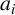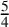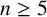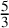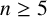Refine search
Actions for selected content:
28927 results in Differential and integral equations, dynamical systems and control theory
4 - Regular Sturm–Liouville Theory and Boundary Value Problems
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 111-140
-
- Chapter
- Export citation
1 - First- and Second-Order ODE
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 3-46
-
- Chapter
- Export citation
References
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 353-356
-
- Chapter
- Export citation
Preface
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp xi-xiv
-
- Chapter
- Export citation
9 - Heat Equation
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 285-306
-
- Chapter
- Export citation
7 - Classification of Partial Differential Equations
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 235-246
-
- Chapter
- Export citation
5 - Qualitative Theory
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 141-182
-
- Chapter
- Export citation
Contents
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp vii-x
-
- Chapter
- Export citation
8 - Laplace and Poisson Equations
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 247-284
-
- Chapter
- Export citation
6 - First-Order Partial Differential Equations
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 185-234
-
- Chapter
- Export citation
Index
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 357-359
-
- Chapter
- Export citation
11 - Wave Equation in Higher Dimensions
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp 329-352
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp xv-xvi
-
- Chapter
- Export citation
List of Illustrations
-
- Book:
- Notes, Problems and Solutions in Differential Equations
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025, pp xxi-xxii
-
- Chapter
- Export citation
INTEGRABLE MODULES OVER QUANTUM SYMMETRIC PAIR COIDEAL SUBALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 05 June 2025, pp. 1-26
-
- Article
- Export citation
ETS volume 45 issue 7 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 04 June 2025, pp. f1-f2
- Print publication:
- July 2025
-
- Article
-
- You have access
- Export citation
SIMPLE TRACIALLY
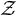 $\mathcal {Z}$-ABSORBING C*-ALGEBRAS
$\mathcal {Z}$-ABSORBING C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 04 June 2025, pp. 1-45
-
- Article
- Export citation
ETS volume 45 issue 7 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 04 June 2025, pp. b1-b2
- Print publication:
- July 2025
-
- Article
-
- You have access
- Export citation
IMPROVED LOWER BOUNDS FOR STRONG n-CONJECTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 02 June 2025, pp. 61-81
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Inverse Problems and Applications
- Inside Out II
-
- Published online:
- 30 May 2025
- Print publication:
- 17 December 2012