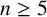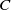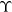Refine search
Actions for selected content:
28952 results in Differential and integral equations, dynamical systems and control theory
ETS volume 45 issue 7 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 04 June 2025, pp. f1-f2
- Print publication:
- July 2025
-
- Article
-
- You have access
- Export citation
SIMPLE TRACIALLY
 $\mathcal {Z}$-ABSORBING C*-ALGEBRAS
$\mathcal {Z}$-ABSORBING C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 04 June 2025, pp. 2135-2179
- Print publication:
- November 2025
-
- Article
- Export citation
ETS volume 45 issue 7 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 04 June 2025, pp. b1-b2
- Print publication:
- July 2025
-
- Article
-
- You have access
- Export citation
IMPROVED LOWER BOUNDS FOR STRONG n-CONJECTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 02 June 2025, pp. 61-81
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Inverse Problems and Applications
- Inside Out II
-
- Published online:
- 30 May 2025
- Print publication:
- 17 December 2012
INFLUENCE OF NOISE-INDUCED MODULATIONS ON THE TIMING STABILITY OF PASSIVELY MODE-LOCKED SEMICONDUCTOR LASER SUBJECT TO OPTICAL FEEDBACK
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 29 May 2025, e22
-
- Article
- Export citation
A multiscale model for espresso brewing: Asymptotic analysis and numerical simulation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cahn–Hilliard equations with singular potential, reaction term and pure phase initial datum
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth orbit equivalence rigidity for dissipative geodesic flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 26 May 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable functional CLT for deterministic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 26 May 2025, pp. 3192-3222
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gelfand–Tsetlin crystals
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 May 2025, pp. 1-14
-
- Article
- Export citation
Agafonov’s theorem for finite and infinite alphabets and probability distributions different from equidistribution
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 3506-3539
- Print publication:
- November 2025
-
- Article
- Export citation
ALPHA–DELTA TRANSITIONS IN CORTICAL RHYTHMS AS GRAZING BIFURCATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 21 May 2025, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIFFRACTION OF THE PRIMES AND OTHER SETS OF ZERO DENSITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 202-245
- Print publication:
- October 2025
-
- Article
- Export citation
Homological full-and-faithfulness of comodule inclusion and contramodule forgetful functors
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POSITIVE DENSITY FOR CONSECUTIVE RUNS OF SUMS OF TWO SQUARES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1995-2046
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JAZ volume 118 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. f1-f2
- Print publication:
- June 2025
-
- Article
-
- You have access
- Export citation
JAZ volume 118 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. b1-b2
- Print publication:
- June 2025
-
- Article
-
- You have access
- Export citation
INDEX
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 407-408
- Print publication:
- June 2025
-
- Article
- Export citation
BIFURCATION ANALYSIS OF THE EFFECT OF TYRE INFLATION PRESSURE ON WHEEL SHIMMY WITH MULTIPLE TYRE PROPERTIES CONSIDERED
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 16 May 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation