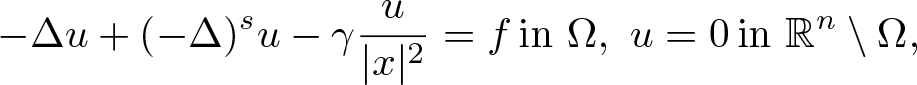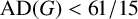Refine search
Actions for selected content:
28952 results in Differential and integral equations, dynamical systems and control theory
Homogenised models of nutrient transport in a fibrous bioreactor scaffold
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 21 April 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASYMPTOTIC DIMENSION AND GEOMETRIC DECOMPOSITIONS IN DIMENSIONS 3 AND 4
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 176-201
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hereditarily frequently hypercyclic operators and disjoint frequent hypercyclicity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 16 April 2025, pp. 3021-3072
- Print publication:
- October 2025
-
- Article
- Export citation
Optimal transport on gas networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Notes, Problems and Solutions in Differential Equations
-
- Published online:
- 15 April 2025
- Print publication:
- 05 June 2025
GENERAL HYPERPLANE SECTIONS OF LOG CANONICAL THREEFOLDS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1867-1894
- Print publication:
- September 2025
-
- Article
- Export citation
Instability of axisymmetric flow in thermocapillary liquid bridges: Kinetic and thermal energy budgets for two-phase flow with temperature-dependent material properties – CORRIGENDUM
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal control of a reaction-diffusion epidemic model with non-compliance
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regularity of quasigeodesics characterizes hyperbolicity
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $ \epsilon $-ISOMORPHISMS FOR RANK ONE
$ \epsilon $-ISOMORPHISMS FOR RANK ONE  $( \varphi , \Gamma )$-MODULES OVER LUBIN-TATE ROBBA RINGS
$( \varphi , \Gamma )$-MODULES OVER LUBIN-TATE ROBBA RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1895-1994
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pattern formation with jump discontinuity in a predator–prey model with Holling-II functional response
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sobolev regularity of the inverse for minimizers of the neo-Hookean energy satisfying condition INV
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-21
-
- Article
- Export citation
On mixed local–nonlocal problems with Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-34
-
- Article
- Export citation
JMJ volume 24 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. b1-b2
- Print publication:
- May 2025
-
- Article
-
- You have access
- Export citation
JMJ volume 24 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. f1-f2
- Print publication:
- May 2025
-
- Article
-
- You have access
- Export citation
MULTIPLE LOCAL AND GLOBAL BIFURCATIONS AND THEIR ROLE IN QUORUM SENSING DYNAMICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 09 April 2025, e17
-
- Article
- Export citation
GENERIC PLANAR PHASE RESETTING NEAR A PHASELESS POINT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 08 April 2025, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modulus of continuity of invariant densities and entropies for piecewise expanding maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 2976-2991
- Print publication:
- October 2025
-
- Article
- Export citation
SMALL VALUES AND FORBIDDEN VALUES FOR THE FOURIER ANTI-DIAGONAL CONSTANT OF A FINITE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 297-316
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spherical normal forms for germs of parabolic line biholomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 3255-3304
- Print publication:
- October 2025
-
- Article
- Export citation