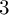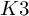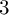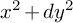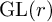Refine search
Actions for selected content:
28954 results in Differential and integral equations, dynamical systems and control theory
ANALYSIS OF A DISCRETIZED FRACTIONAL-ORDER PREY–PREDATOR MODEL UNDER WIND EFFECT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spatio-temporal dynamics of a lattice prey–predator system with non-local diffusion in a periodic habitat
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 March 2025, pp. 1-43
-
- Article
- Export citation
Characterization of the tree cycles with minimum positive entropy for any period
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 3148-3191
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GMJ volume 67 issue 2 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 28 March 2025, pp. b1-b2
- Print publication:
- May 2025
-
- Article
-
- You have access
- Export citation
Every locally compact group is the outer automorphism group of a II1 factor
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 March 2025, pp. 1-12
-
- Article
- Export citation
GMJ volume 67 issue 2 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 28 March 2025, pp. f1-f2
- Print publication:
- May 2025
-
- Article
-
- You have access
- Export citation
How to beat a Bayesian adversary
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 28 March 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TEICHMÜLLER CURVES IN HYPERELLIPTIC COMPONENTS OF MEROMORPHIC STRATA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 26 March 2025, pp. 1521-1546
- Print publication:
- July 2025
-
- Article
- Export citation
JAZ volume 118 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. f1-f2
- Print publication:
- April 2025
-
- Article
-
- You have access
- Export citation
JAZ volume 118 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. b1-b2
- Print publication:
- April 2025
-
- Article
-
- You have access
- Export citation
TWISTED BLANCHFIELD PAIRINGS AND TWISTED SIGNATURES II: RELATION TO CASSON-GORDON INVARIANTS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 20 March 2025, pp. 1139-1195
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DEGREE OF IRRATIONALITY OF LOW GENUS
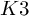 $K3$ SURFACES
$K3$ SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 19 March 2025, pp. 627-662
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ESTIMATION OF MEAN SQUARED ERRORS OF NON-BINARY A/D ENCODERS THROUGH FREDHOLM DETERMINANTS OF PIECEWISE-LINEAR TRANSFORMATIONS II: GENERAL CASE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 19 March 2025, e14
-
- Article
- Export citation
STATED SKEIN MODULES OF 3-MANIFOLDS AND TQFT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 19 March 2025, pp. 663-703
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON K-STABILITY OF CALABI-YAU FIBRATIONS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 19 March 2025, pp. 961-1019
- Print publication:
- May 2025
-
- Article
- Export citation
3D Navier–Stokes–Voigt equations with damping and double delays on unbounded domains: Well-posedness, pullback attractors, and limit measures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1-39
-
- Article
- Export citation
COVERING INTEGERS BY
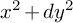 $x^2 + dy^2$
$x^2 + dy^2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 847-889
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROJECTIVELY FLAT FOLIATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 763-812
- Print publication:
- May 2025
-
- Article
- Export citation
NOMBRE DE PETITS POINTS SUR UNE VARIÉTÉ ABÉLIENNE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 705-761
- Print publication:
- May 2025
-
- Article
- Export citation
SIMPLE TYPE THEORY FOR METAPLECTIC COVERS OF
 $\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
$\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1263-1335
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation


















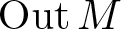
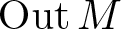

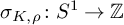
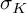

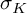
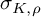
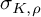
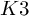
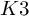
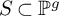
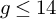
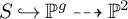 of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most
of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most 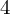
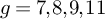
 of degree
of degree