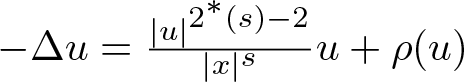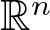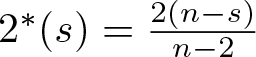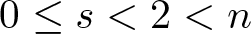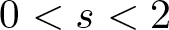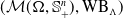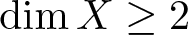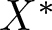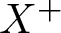Refine search
Actions for selected content:
28954 results in Differential and integral equations, dynamical systems and control theory
Semisimple random walks on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 3090-3147
- Print publication:
- October 2025
-
- Article
- Export citation
Unique compact representation of magnetic fields using truncated solid harmonic expansions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1012-1039
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-additive derived functors via chain resolutions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 February 2025, pp. 423-466
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theory of heat equations for sigma functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 February 2025, pp. 365-422
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a perturbed critical semilinear equation with singularity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 February 2025, pp. 1-35
-
- Article
- Export citation
Are free groups of different ranks bi-invariantly quasi-isometric?
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 356-364
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLYNOMIALS REPRESENTED BY NORM FORMS VIA THE BETA SIEVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 25 February 2025, pp. 1463-1519
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An elliptic operator with a nonlocal term: maximum principle, principal eigenvalue, and applications to a logistic equation with indefinite weight
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-38
-
- Article
- Export citation
Transitive mappings on the Cantor fan
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 2601-2635
- Print publication:
- September 2025
-
- Article
- Export citation
Global well-posedness and Turing–Hopf bifurcation of prey-taxis systems with hunting cooperation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting problems from the viewpoint of ergodic theory: from primitive integer points to simple closed curves
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1281-1328
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple solutions for some classes of non-linear elliptic equations with variable exponents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-51
-
- Article
- Export citation
Renormalization of circle maps and smoothness of Arnold tongues
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 2845-2889
- Print publication:
- September 2025
-
- Article
- Export citation
On a general matrix-valued unbalanced optimal transport problem
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On partial rigidity of
 $\mathcal {S}$-adic subshifts
$\mathcal {S}$-adic subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 2724-2764
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two dynamical approaches to the notion of exponential separation for random systems of delay differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of non-trivial embeddings of interval exchange transformations into piecewise isometries
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 2194-2232
- Print publication:
- July 2025
-
- Article
- Export citation
Forman–Ricci communicability curvature of graphs and networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the
 $\mu$-invariant of two-variable
$\mu$-invariant of two-variable  $2$-adic
$2$-adic  $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 325-355
- Print publication:
- September 2025
-
- Article
- Export citation
SU(2)-bundles over highly connected 8-manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 February 2025, pp. 1-30
-
- Article
- Export citation