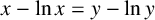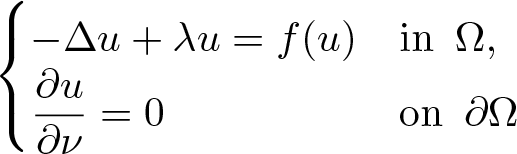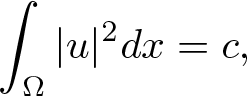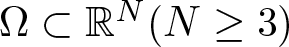Refine search
Actions for selected content:
28952 results in Differential and integral equations, dynamical systems and control theory
MIXED BOUNDARY VALUE PROBLEM IN MICROFLUIDICS: THE AVER’YANOV–BLUNT MODEL REVISITED
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 07 April 2025, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of mapping class groups MOD powers of twists
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-71
-
- Article
- Export citation
ETS volume 45 issue 5 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. f1-f2
- Print publication:
- May 2025
-
- Article
-
- You have access
- Export citation
Periodic points of rational area-preserving homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 2890-2907
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adversarial consistency and the uniqueness of the adversarial bayes classifier
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 04 April 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 45 issue 5 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. b1-b2
- Print publication:
- May 2025
-
- Article
-
- You have access
- Export citation
A hyperbolic free-by-cyclic group determined by its finite quotients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 500-502
- Print publication:
- September 2025
-
- Article
- Export citation
The Klein bottle has stably unbounded homeomorphism group
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 494-499
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Codazzi and totally umbilical hypersurfaces in
 $\mathrm {Sol}_1^4$
$\mathrm {Sol}_1^4$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 April 2025, pp. 487-493
- Print publication:
- September 2025
-
- Article
- Export citation
PERIODIC SOLUTIONS FOR A PAIR OF DELAY-COUPLED ACTIVE THETA NEURONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Borel complexity of sets of points with prescribed Birkhoff averages in Polish dynamical systems with a specification property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 2695-2723
- Print publication:
- September 2025
-
- Article
- Export citation
ANALYTICAL APPROXIMATIONS OF LOTKA–VOLTERRA INTEGRALS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NLP verification: towards a general methodology for certifying robustness
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Newton–Maclaurin type inequalities for linear combinations of elementary symmetric functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-18
-
- Article
- Export citation
Remark on the local well-posedness for NLS with the modulated dispersion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-12
-
- Article
- Export citation
Numerical solution of a PDE arising from prediction with expert advice
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DYNAMICAL ANALYSIS OF A PARAMETRICALLY FORCED MAGNETO-MECHANICAL OSCILLATOR
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solutions with prescribed mass for L2-supercritical NLS equations under Neumann boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYSIS OF A DISCRETIZED FRACTIONAL-ORDER PREY–PREDATOR MODEL UNDER WIND EFFECT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spatio-temporal dynamics of a lattice prey–predator system with non-local diffusion in a periodic habitat
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 March 2025, pp. 1-43
-
- Article
- Export citation