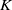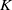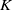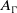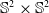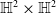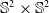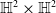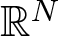Refine search
Actions for selected content:
28952 results in Differential and integral equations, dynamical systems and control theory
Cartesian closed varieties II: links to algebra and self-similarity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2025, pp. 1-45
-
- Article
- Export citation
DELAYED HOPF BIFURCATIONS IN REACTION–DIFFUSION SYSTEMS IN TWO SPACE DIMENSIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 13 May 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Automorphism groups and signatures of smooth septic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-22
-
- Article
- Export citation
The Formanek-Procesi group with base a right-angled Artin group: Lie algebra and residual nilpotence
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-22
-
- Article
- Export citation
Orbit separation dimension as complexity measure for primitive inflation tilings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 2992-3020
- Print publication:
- October 2025
-
- Article
- Export citation
A flower theorem in dimension two
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 08 May 2025, pp. 3223-3254
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONTRACTING ENDOMORPHISMS OF VALUED FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 08 May 2025, pp. 2047-2106
- Print publication:
- September 2025
-
- Article
- Export citation
FONCTIONS ADDITIVES EN BASE DE CANTOR LE LONG DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 06 May 2025, pp. 1807-1865
- Print publication:
- September 2025
-
- Article
- Export citation
ETS volume 45 issue 6 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 05 May 2025, pp. b1-b2
- Print publication:
- June 2025
-
- Article
-
- You have access
- Export citation
ETS volume 45 issue 6 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 05 May 2025, pp. f1-f2
- Print publication:
- June 2025
-
- Article
-
- You have access
- Export citation
On hypersurfaces of
 $\mathbb{S}^2\times \mathbb{S}^2$ and
$\mathbb{S}^2\times \mathbb{S}^2$ and 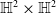 $\mathbb{H}^2\times \mathbb{H}^2$ with recurrent Ricci tensor
$\mathbb{H}^2\times \mathbb{H}^2$ with recurrent Ricci tensor
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 30 April 2025, pp. 1-21
-
- Article
- Export citation
Homomorphisms from aperiodic subshifts to subshifts with the finite extension property
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 3073-3089
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-existence theorems for quasilinear elliptic equations with weights
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-33
-
- Article
- Export citation
On Fock covariance for product systems and the reduced Hao–Ng isomorphism problem by discrete actions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-53
-
- Article
- Export citation
Integral constraints in multiple scales problems with a slowly varying microstructure
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 25 April 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MOCK PLECTIC POINTS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 24 April 2025, pp. 2107-2131
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the long-time asymptotics of the modified Camassa–Holm equation with step-like initial data
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 23 April 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global dynamics for the generalised chemotaxis-Navier–Stokes system in
 $\mathbb{R}^3$
$\mathbb{R}^3$
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 22 April 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Diagrammatics for the smallest quantum coideal and Jones–Wenzl projectors
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 April 2025, pp. 1-20
-
- Article
- Export citation
The Real Teapot
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 2945-2975
- Print publication:
- October 2025
-
- Article
- Export citation