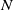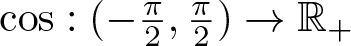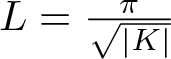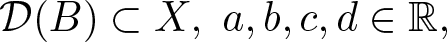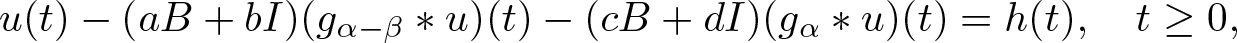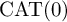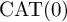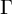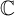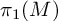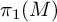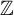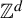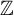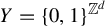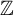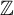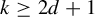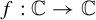Refine search
Actions for selected content:
28954 results in Differential and integral equations, dynamical systems and control theory
Automorphisms of fine curve graphs for nonorientable surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 16 January 2025, pp. 232-244
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entire maps with rational preperiodic points and multipliers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 15 January 2025, pp. 2636-2658
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4-Torsion classes in the integral cohomology of oriented Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 January 2025, pp. 1-43
-
- Article
- Export citation
A Bonnet–Myers rigidity theorem for globally hyperbolic Lorentzian length spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Well-posedness for strongly damped abstract Cauchy problems of fractional order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-27
-
- Article
- Export citation
ERRATUM TO THE PAPER ‘BREUIL–KISIN–FARGUES MODULES WITH COMPLEX MULTIPLICATION’
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 585-586
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
NONLINEAR MODULATION OF RANDOM WAVE SPECTRA FOR SURFACE-GRAVITY WAVES WITH LINEAR SHEAR CURRENTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 10 January 2025, pp. 222-237
-
- Article
- Export citation
Spatio-temporal behaviour of SIR models with cross-diffusion and vital dynamics
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 972-992
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dichotomy spectrum and reducibility for mean hyperbolic systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 January 2025, pp. 1-19
-
- Article
- Export citation
ETS volume 45 issue 2 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. b1-b2
- Print publication:
- February 2025
-
- Article
-
- You have access
- Export citation
Functions with small BMO norm
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 January 2025, pp. 1-15
-
- Article
- Export citation
ETS volume 45 issue 2 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. f1-f2
- Print publication:
- February 2025
-
- Article
-
- You have access
- Export citation
Bounds for equilibrium states on amenable group subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 2414-2438
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROPER
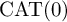 $\mathrm {CAT(0)}$ ACTIONS OF UNIPOTENT-FREE LINEAR GROUPS
$\mathrm {CAT(0)}$ ACTIONS OF UNIPOTENT-FREE LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 587-601
- Print publication:
- March 2025
-
- Article
- Export citation
An embedding theorem for multidimensional subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 1870-1914
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lavaurs algorithm for cubic symmetric polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2314-2340
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mean field limits of co-evolutionary signed heterogeneous networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 January 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transcendental Julia sets of minimal Hausdorff dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2341-2413
- Print publication:
- August 2025
-
- Article
- Export citation
First Ruelle resonance for an Anosov flow with smooth potential
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2439-2475
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Examples of ergodic cylindrical cascades over a two-dimensional torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 02 January 2025, pp. 1929-1946
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation