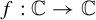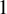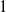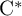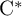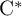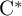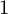Refine search
Actions for selected content:
28957 results in Differential and integral equations, dynamical systems and control theory
Transcendental Julia sets of minimal Hausdorff dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2341-2413
- Print publication:
- August 2025
-
- Article
- Export citation
First Ruelle resonance for an Anosov flow with smooth potential
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2439-2475
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Examples of ergodic cylindrical cascades over a two-dimensional torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 02 January 2025, pp. 1929-1946
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JMJ volume 24 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. b1-b2
- Print publication:
- January 2025
-
- Article
-
- You have access
- Export citation
GMJ volume 67 issue 1 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 31 January 2025, pp. f1-f2
- Print publication:
- January 2025
-
- Article
-
- You have access
- Export citation
JMJ volume 24 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. f1-f2
- Print publication:
- January 2025
-
- Article
-
- You have access
- Export citation
GMJ volume 67 issue 1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 31 January 2025, pp. b1-b2
- Print publication:
- January 2025
-
- Article
-
- You have access
- Export citation
The two membranes problem in a regular tree
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 December 2024, pp. 1-30
-
- Article
- Export citation
Joining properties of automorphisms disjoint with all ergodic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 1998-2022
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some remarks about self-products and entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 2183-2193
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISSIPATION OF WAVE ENERGY AND MITIGATION OF WAVE FORCE BY MULTIPLE FLEXIBLE POROUS PLATES
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 26 December 2024, pp. 258-284
-
- Article
- Export citation
A Szemerédi type theorem for sets of positive density in approximate lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2023-2053
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double EPW sextics associated with Gushel–Mukai surfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-22
-
- Article
- Export citation
Linear repetitivity beyond abelian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1947-1997
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New classes of quasigeodesic Anosov flows in
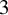 $3$-manifolds
$3$-manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2095-2131
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finely quasiconformal mappings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-25
-
- Article
- Export citation
Rank-one systems, flexible classes and Shannon orbit equivalence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2132-2182
- Print publication:
- July 2025
-
- Article
- Export citation
Discrete-to-continuum limits of optimal transport with linear growth on periodic graphs
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RANKS OF SOFT OPERATORS IN NOWHERE SCATTERED
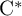 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 371-410
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - Are the Central Configurations Finite?
- from Part Two - The Questions
-
- Book:
- Four Open Questions for the <i>N</i>-Body Problem
- Published online:
- 12 December 2024
- Print publication:
- 19 December 2024, pp 75-100
-
- Chapter
- Export citation