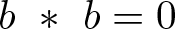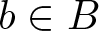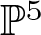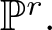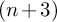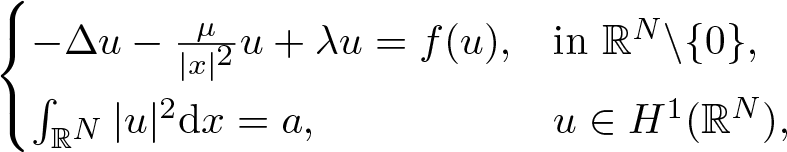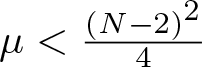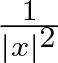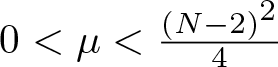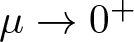Refine search
Actions for selected content:
28957 results in Differential and integral equations, dynamical systems and control theory
Appendix A - Geometric Mechanics
-
- Book:
- Four Open Questions for the <i>N</i>-Body Problem
- Published online:
- 12 December 2024
- Print publication:
- 19 December 2024, pp 217-227
-
- Chapter
- Export citation
Appendix D - The Orthogonal Group and Its Lie Algebra
-
- Book:
- Four Open Questions for the <i>N</i>-Body Problem
- Published online:
- 12 December 2024
- Print publication:
- 19 December 2024, pp 262-263
-
- Chapter
- Export citation
Appendix B - Reduction and Poisson Brackets
-
- Book:
- Four Open Questions for the <i>N</i>-Body Problem
- Published online:
- 12 December 2024
- Print publication:
- 19 December 2024, pp 228-241
-
- Chapter
- Export citation
Lyapunov stability of non-isolated equilibria for strongly irreversible Allen–Cahn equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-21
-
- Article
- Export citation
Finite presentability of twisted Brin–Thompson groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on right-nil and strong-nil skew braces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-9
-
- Article
- Export citation
Propagation dynamics for an epidemic patch model with variable incubation period
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 18 December 2024, pp. 948-971
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ORDER-PRESERVING EXTENSIONS OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 17 December 2024, pp. 91-107
- Print publication:
- February 2025
-
- Article
- Export citation
On the Hilbert scheme of smooth curves of degree d = 15 in
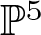 $\mathbb{P}^5$
$\mathbb{P}^5$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-38
-
- Article
- Export citation

Four Open Questions for the N-Body Problem
-
- Published online:
- 12 December 2024
- Print publication:
- 19 December 2024
FINITE-DIMENSIONAL DIFFERENTIAL-ALGEBRAIC PERMUTATION GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 603-626
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Daugavet and Delta-constants of points in Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2024, pp. 1-35
-
- Article
- Export citation
Fractional time differential equations as a singular limit of the Kobayashi–Warren–Carter system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 December 2024, pp. 1-37
-
- Article
- Export citation
Birkhoff spectrum for diagonally self-affine sets and digit frequencies for GLS systems with redundancy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Normalized ground state solutions for critical growth Schrödinger equations with Hardy potential
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-30
-
- Article
- Export citation
Shadowing and hyperbolicity for linear delay difference equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-30
-
- Article
- Export citation
Continuum limit for interacting systems on adaptive networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 December 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Well-posedness for nonlinear SPDEs with strongly continuous perturbation - ERRATUM
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 December 2024, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 45 issue 1 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. b1-b2
- Print publication:
- January 2025
-
- Article
-
- You have access
- Export citation
On the existence of solutions to adversarial training in multiclass classification
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 03 December 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation