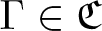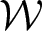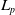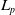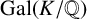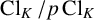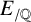Refine search
Actions for selected content:
28957 results in Differential and integral equations, dynamical systems and control theory
SYMMETRY RESTORATION IN COLLISIONS OF SOLITONS IN FRACTIONAL COUPLERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 December 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal strong foliations in skew-products of iterated function systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 2273-2313
- Print publication:
- August 2025
-
- Article
- Export citation
Strongly outer actions of certain torsion-free amenable groups on the Razak–Jacelon algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 December 2024, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 45 issue 1 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. f1-f2
- Print publication:
- January 2025
-
- Article
-
- You have access
- Export citation
HARMONIC RESONANCE OF SHORT-CRESTED GRAVITY WAVES ON DEEP WATER: ON THEIR PERSISTENCY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 December 2024, e1
-
- Article
- Export citation
Transference of multilinear Fourier and Schur multipliers acting on noncommutative
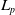 $L_p$-spaces for non-unimodular groups
$L_p$-spaces for non-unimodular groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 197-223
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integrability of special quadratic systems with invariant hyperbolas
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-27
-
- Article
- Export citation
CLASS GROUP STATISTICS FOR TORSION FIELDS GENERATED BY ELLIPTIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 245-264
- Print publication:
- April 2025
-
- Article
- Export citation
On a class of bivariate distributions built of q-ultraspherical polynomials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-34
-
- Article
- Export citation
Analysis of a model describing bacterial colony expansion in radial geometry driven by chemotaxis
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 910-947
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasidiagonals in strata of translation surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 2233-2248
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generic properties of topological groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the Winterbottom shape
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JAZ volume 117 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 02 December 2024, pp. f1-f2
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation
Vanishing of Nil-terms and negative K-theory for additive categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1945-2023
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRM volume 154 issue 6 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 March 2025, pp. f1-f2
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation
Poincaré complex diagonals and the Bass trace conjecture – CORRIGENDUM
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 March 2025, p. 1841
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JAZ volume 117 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 02 December 2024, pp. b1-b2
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation
INDEX
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 02 December 2024, p. 392
- Print publication:
- December 2024
-
- Article
- Export citation
PRM volume 154 issue 6 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 March 2025, pp. b1-b2
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation