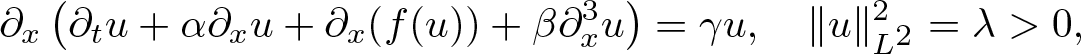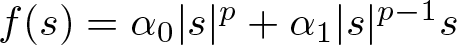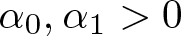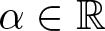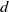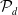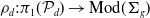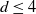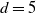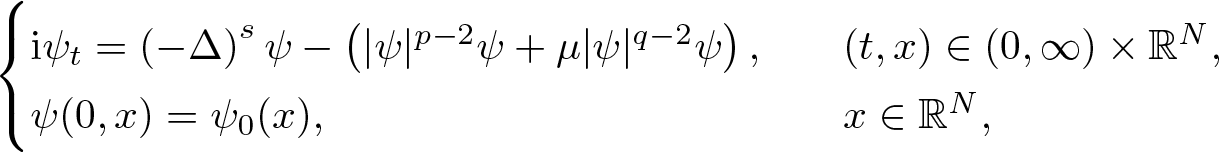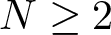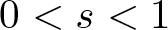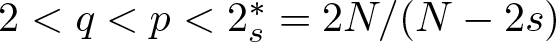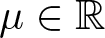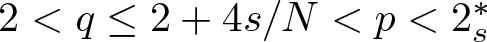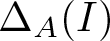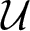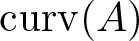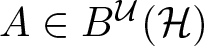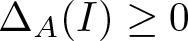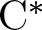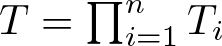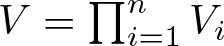Refine search
Actions for selected content:
28962 results in Differential and integral equations, dynamical systems and control theory
PRM volume 154 issue 6 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 March 2025, pp. f1-f2
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation
Poincaré complex diagonals and the Bass trace conjecture – CORRIGENDUM
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 March 2025, p. 1841
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JAZ volume 117 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 02 December 2024, pp. b1-b2
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation
INDEX
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 02 December 2024, p. 392
- Print publication:
- December 2024
-
- Article
- Export citation
PRM volume 154 issue 6 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 March 2025, pp. b1-b2
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation
Andrew Ranicki
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 March 2025, pp. 1635-1638
- Print publication:
- December 2024
-
- Article
- Export citation
Isometric dilations for representations of product systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On finite presentability of subsemigroups of the monogenic free inverse semigroup
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 28 November 2024, pp. 185-196
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral stability of constrained solitary waves for a generalized Ostrovsky equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-32
-
- Article
- Export citation
On the monodromy group of the family of smooth quintic plane curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 28 November 2024, pp. 163-184
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Instability of standing waves for fractional NLS with combined nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-29
-
- Article
- Export citation
Numerical invariants on twisted noncommutative polyballs: curvature and multiplicity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-54
-
- Article
- Export citation
The admissible KMS bundles on classifiable C⁎-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kolmogorov’s theorem for degenerate Hamiltonian systems with Hölder continuous parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-36
-
- Article
- Export citation
Well-posedness of quasilinear parabolic equations in time-weighted spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-33
-
- Article
- Export citation
Minimal isometric dilations and operator models for the polydisc
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-40
-
- Article
- Export citation
Geometry of tropical extensions of hyperfields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant parametrized topological complexity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-24
-
- Article
- Export citation
Semiabelian varieties and transcendence on Weierstrass sigma functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 107-113
- Print publication:
- January 2025
-
- Article
- Export citation
Local regularity for nonlocal double phase equations in the Heisenberg group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-37
-
- Article
- Export citation