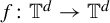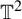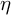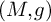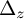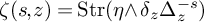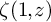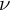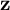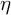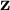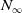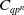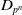Refine search
Actions for selected content:
28885 results in Differential and integral equations, dynamical systems and control theory
EFFECT OF NONUNIFORM POROSITY IN CURVED BREAKWATER ON WATER WAVES
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 21 October 2024, pp. 201-221
-
- Article
- Export citation
IRROTATIONAL FLOW DUE TO FORCED OSCILLATIONS OF A BUBBLE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 18 October 2024, pp. 152-180
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a weighted anisotropic eigenvalue problem
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 October 2024, pp. 72-85
- Print publication:
- January 2025
-
- Article
- Export citation
IMPLICIT–EXPLICIT TIME INTEGRATION METHOD FOR FRACTIONAL ADVECTION–DIFFUSION-REACTION EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 16 October 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EFFECT OF EXTERNAL HARMONIC VIBRATION ON THE FORMATION OF SOLITARY WAVES IN FALLING TWO-LAYER LIQUID FILMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 16 October 2024, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of Lyapunov exponents for derived from Anosov diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 1444-1460
- Print publication:
- May 2025
-
- Article
- Export citation
Global rigidity of smooth
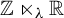 ${\mathbb{Z}}\ltimes _{\unicode{x3bb}}{\mathbb{R}}$-actions on
${\mathbb{Z}}\ltimes _{\unicode{x3bb}}{\mathbb{R}}$-actions on  ${\mathbb{T}}^{2}$
${\mathbb{T}}^{2}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 1161-1176
- Print publication:
- April 2025
-
- Article
- Export citation
Effective dynamical systems beyond dimension zero and factors of SFTs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1329-1369
- Print publication:
- May 2025
-
- Article
- Export citation
Geometric properties of disintegration of measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1619-1648
- Print publication:
- May 2025
-
- Article
- Export citation
ZETA INVARIANTS OF MORSE FORMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 411-480
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Travelling wavefronts for the Belousov–Zhabotinsky system with non-local delayed interaction
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 738-774
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Early warning signs for SPDEs with continuous spectrum
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 665-704
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Construction of smooth isomorphic and finite-to-one extensions of irrational rotations which are not almost automorphic
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1224-1245
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 44 issue 11 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. b1-b2
- Print publication:
- November 2024
-
- Article
-
- You have access
- Export citation
The combinatorics of
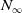 $N_\infty$ operads for
$N_\infty$ operads for 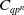 $C_{qp^n}$ and
$C_{qp^n}$ and 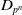 $D_{p^n}$
$D_{p^n}$
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 50-66
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 44 issue 11 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. f1-f2
- Print publication:
- November 2024
-
- Article
-
- You have access
- Export citation
Classification of multiplication modules over multiplication rings with finitely many minimal primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 67-71
- Print publication:
- January 2025
-
- Article
- Export citation
Volume and Euler classes in bounded cohomology of transformation groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 02 October 2024, pp. 34-49
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRM volume 154 issue 5 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 09 October 2024, pp. b1-b2
- Print publication:
- October 2024
-
- Article
-
- You have access
- Export citation
JAZ volume 117 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 09 October 2024, pp. b1-b2
- Print publication:
- October 2024
-
- Article
-
- You have access
- Export citation
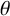
 ) and the Zimm chain solution (
) and the Zimm chain solution ( ). Numerical simulations of the viscoelastic channel flow effectively capture the nonhomogeneous regions of high viscosity at low fluid inertia (or the so-called “spatiotemporal macrostructures”), experimentally observed in the flow-instability transition of subdiffusive flows.
). Numerical simulations of the viscoelastic channel flow effectively capture the nonhomogeneous regions of high viscosity at low fluid inertia (or the so-called “spatiotemporal macrostructures”), experimentally observed in the flow-instability transition of subdiffusive flows.