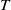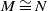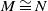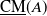Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
12 - LU (Spectral) Factorization
- from Part II - Further Contributions to Matrix Theory
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 185-201
-
- Chapter
- Export citation
Part II - Further Contributions to Matrix Theory
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 183-184
-
- Chapter
- Export citation
1 - A First Example: Optimal Quadratic Control
- from Part I - Lectures on Basics with Examples
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 3-20
-
- Chapter
- Export citation
16 - Constrained Model Reduction
- from Part II - Further Contributions to Matrix Theory
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 254-276
-
- Chapter
- Export citation
17 - Isometric Embedding for Causal Contractions
- from Part II - Further Contributions to Matrix Theory
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 277-291
-
- Chapter
- Export citation
References
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 300-303
-
- Chapter
- Export citation
14 - The Scattering Picture
- from Part II - Further Contributions to Matrix Theory
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 223-241
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp xxiii-xxiv
-
- Chapter
- Export citation
Appendix: Data Model and Implementations
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 292-299
-
- Chapter
- Export citation
15 - Constrained Interpolation
- from Part II - Further Contributions to Matrix Theory
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 242-253
-
- Chapter
- Export citation
13 - Matrix Schur Interpolation
- from Part II - Further Contributions to Matrix Theory
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 202-222
-
- Chapter
- Export citation
10 - Polynomial Representations
- from Part I - Lectures on Basics with Examples
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 154-168
-
- Chapter
- Export citation
Preface
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp xi-xxii
-
- Chapter
- Export citation
Part I - Lectures on Basics with Examples
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 1-2
-
- Chapter
- Export citation
Contents
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp v-x
-
- Chapter
- Export citation
6 - Elementary Operations
- from Part I - Lectures on Basics with Examples
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 87-94
-
- Chapter
- Export citation
8 - Inner−Outer Factorization
- from Part I - Lectures on Basics with Examples
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 115-135
-
- Chapter
- Export citation
A sub-functor for Ext and Cohen–Macaulay associated graded modules with bounded multiplicity-II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 30 October 2024, pp. 86-106
- Print publication:
- January 2025
-
- Article
- Export citation
SPANNING TREES IN
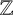 $\mathbb {Z}$-COVERS OF A FINITE GRAPH AND MAHLER MEASURES
$\mathbb {Z}$-COVERS OF A FINITE GRAPH AND MAHLER MEASURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 108-144
- Print publication:
- February 2025
-
- Article
- Export citation
A diffusive plant-sulphide model: spatio-temporal dynamics contrast between discrete and distributed delay
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 811-828
-
- Article
-
- You have access
- Open access
- HTML
- Export citation