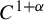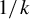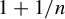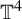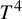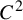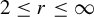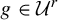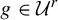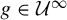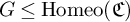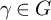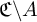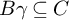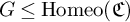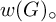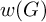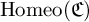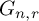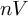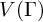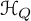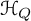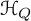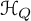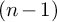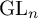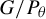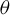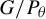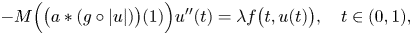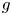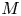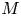Refine search
Actions for selected content:
28972 results in Differential and integral equations, dynamical systems and control theory
On the critical regularity of nilpotent groups acting on the interval: the metabelian case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 24 September 2024, pp. 1177-1198
- Print publication:
- April 2025
-
- Article
- Export citation
Shub’s example revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 23 September 2024, pp. 894-914
- Print publication:
- March 2025
-
- Article
- Export citation
SUFFICIENT CONDITIONS FOR A GROUP OF HOMEOMORPHISMS OF THE CANTOR SET TO BE TWO-GENERATED
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 2825-2858
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GROUPS AND FIELDS DEFINABLE IN
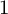 $1$-H-MINIMAL FIELDS
$1$-H-MINIMAL FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 September 2024, pp. 203-248
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DT INVARIANTS FROM VERTEX ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 September 2024, pp. 291-339
- Print publication:
- January 2025
-
- Article
- Export citation
THE SLICE-BENNEQUIN INEQUALITY FOR THE FRACTIONAL DEHN TWIST COEFFICIENT
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 September 2024, pp. 273-289
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PARITY OF CONJUGATE SELF-DUAL REPRESENTATIONS OF INNER FORMS OF
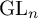 $\operatorname { {GL}}_n$ OVER p-ADIC FIELDS
$\operatorname { {GL}}_n$ OVER p-ADIC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 September 2024, pp. 249-271
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EMBED IN ENSEMBLE TO RIGOROUSLY AND ACCURATELY HOMOGENIZE QUASI-PERIODIC MULTI-SCALE HETEROGENEOUS MATERIAL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYTICALLY PRICING EUROPEAN OPTIONS UNDER A TWO-FACTOR STOCHASTIC INTEREST RATE MODEL WITH A STOCHASTIC LONG-RUN EQUILIBRIUM LEVEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 132-151
-
- Article
- Export citation
Travelling waves with continuous profile for hyperbolic Keller-Segel equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 584-612
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-concentration property of Patterson–Sullivan measures for Anosov subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 884-893
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-linear biphasic mixture model: Existence and uniqueness results
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 161-185
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A unified characterization of convolution coefficients in nonlocal differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
- Export citation
On the quasi-ergodicity of absorbing Markov chains with unbounded transition densities, including random logistic maps with escape – CORRIGENDUM
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 956-960
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
Multifractal analysis of homological growth rates for hyperbolic surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 849-883
- Print publication:
- March 2025
-
- Article
- Export citation
Rigidity of flat holonomies
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1048-1077
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact recovery of community detection in k-community Gaussian mixture models
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 491-523
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal transport through a toll station
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 613-637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPECTRAL CLUSTERING AND LONG TIMESERIES CLASSIFICATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 121-131
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a supersonic-sonic patch arising from the two-dimensional Riemann problem of the compressible Euler equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-40
-
- Article
- Export citation